题目内容
已知双曲线C的中心在原点,抛物线 的焦点是双曲线C的一个焦点,且双曲线经过点
的焦点是双曲线C的一个焦点,且双曲线经过点 ,又知直线
,又知直线 与双曲线C相交于A、B两点.
与双曲线C相交于A、B两点.
(1)求双曲线C的方程;
(2)若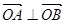 ,求实数k值.
,求实数k值.
 的焦点是双曲线C的一个焦点,且双曲线经过点
的焦点是双曲线C的一个焦点,且双曲线经过点 ,又知直线
,又知直线 与双曲线C相交于A、B两点.
与双曲线C相交于A、B两点.(1)求双曲线C的方程;
(2)若
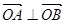 ,求实数k值.
,求实数k值.(1) (2)
(2)
 (2)
(2)
试题分析:(1)抛物线的焦点是(
 ),则双曲线的
),则双曲线的 .………………1分
.………………1分设双曲线方程:
 …………………………2分
…………………………2分解得:
 …………………………5分
…………………………5分(2)联立方程:

当
 ……………………7分(未写△扣1分)
……………………7分(未写△扣1分)由韦达定理:
 ……………………8分
……………………8分设

 代入可得:
代入可得: ,检验合格.……12分
,检验合格.……12分点评:第一小题利用定义首先求出2a也比较简单

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
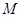 经过定点
经过定点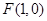 ,且与直线
,且与直线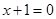 相切。
相切。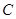 方程;
方程;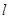 过定点
过定点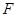 与曲线
与曲线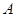 、
、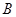 两点:
两点: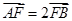 ,求直线
,求直线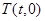 始终在以
始终在以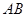 为直径的圆内,求
为直径的圆内,求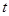 的取值范围。
的取值范围。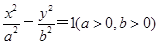 的一条渐近线的倾斜角为
的一条渐近线的倾斜角为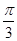 ,离心率为
,离心率为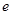 ,则
,则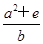 的最小值为( )
的最小值为( ) 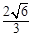
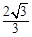
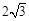
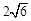
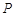 是椭圆
是椭圆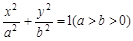 上的一动点,且
上的一动点,且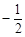 ,则椭圆离心率为
,则椭圆离心率为 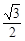
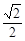
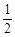
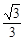
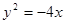 上的焦点
上的焦点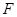 ,点
,点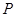 在抛物线上,点
在抛物线上,点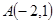 ,则要使
,则要使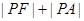 的值最小的点
的值最小的点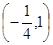
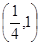
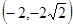
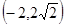
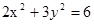 有两个交点 ( )
有两个交点 ( )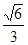 <k<
<k<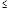 k
k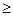
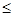 —
—
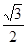

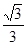
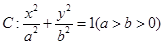 的离心率为
的离心率为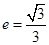 ,以原点为圆心,椭圆短半轴长为半径的圆与直线
,以原点为圆心,椭圆短半轴长为半径的圆与直线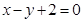 相切,
相切,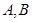 分别是椭圆的左右两个顶点,
分别是椭圆的左右两个顶点,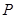 为椭圆
为椭圆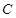 上的动点.
上的动点.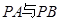 的斜率分别为
的斜率分别为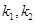 ,求
,求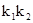 的值。
的值。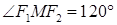 ,则双曲线离心率为
,则双曲线离心率为