题目内容
6.由两个1,两个2,两个3组成的6位数的个数为( )| A. | 45 | B. | 90 | C. | 120 | D. | 360 |
分析 问题等价于从6个位置中各选出2个位置填上相同的1,2,3,由分步计数原理可以解得.
解答 解:问题等价于从6个位置中各选出2个位置填上相同的1,2,3,
所以由分步计数原理有:C62C42C22=90个不同的六位数,
故选:B.
点评 本题考查了分步计数原理,关键是转化,属于中档题.

练习册系列答案
相关题目
17.已知$α∈(-\frac{π}{2},0)$且$sin(\frac{π}{2}+α)=\frac{4}{5}$,则tanα=( )
| A. | $-\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | $-\frac{4}{3}$ | D. | $\frac{4}{3}$ |
18.如图,在梯形ABCD中,AB=3CD,则下列判断正确的是( )
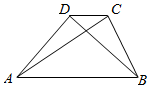

| A. | $\overrightarrow{AB}$=3$\overrightarrow{CD}$ | B. | $\overrightarrow{AC}$=$\frac{1}{3}$$\overrightarrow{AB}$-$\overrightarrow{AD}$ | C. | $\overrightarrow{BD}$=$\overrightarrow{AB}$-$\overrightarrow{AD}$ | D. | $\overrightarrow{BC}$=-$\frac{2}{3}$$\overrightarrow{AB}$+$\overrightarrow{AD}$ |
15.某几何体的三视图如图所示,且该几何体的体积是$\frac{3}{2}$,则正视图中的x的值是( )
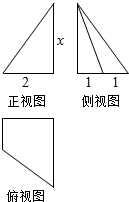

| A. | 2 | B. | $\frac{9}{2}$ | C. | $\frac{3}{2}$ | D. | 3 |
16.定义在R上的函数f(x)满足f(x+1)=2f(x),且当0≤x≤1时,f(x)=x2-x,则$f({-\frac{3}{2}})$=( )
| A. | $-\frac{1}{2}$ | B. | $-\frac{1}{4}$ | C. | $-\frac{1}{8}$ | D. | $-\frac{1}{16}$ |