题目内容
9.椭圆$\frac{{x}^{2}}{3}$+y2=1两焦点之间的距离为2$\sqrt{2}$.分析 根据题意,由椭圆的方程计算可得其焦点坐标,进而可得两焦点之间的距离,即可得答案.
解答 解:根据题意,椭圆的方程为:$\frac{{x}^{2}}{3}$+y2=1,
其焦点坐标为(±$\sqrt{2}$,0),
则两焦点之间的距离为2$\sqrt{2}$;
故答案为:2$\sqrt{2}$.
点评 本题考查椭圆的性质,关键是依据椭圆的标准方程求出焦点坐标.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
20.已知集合A={x|-1≤x<3},B={x∈Z|x2<4},则A∩B=( )
| A. | {0,1} | B. | {-1,0,1} | C. | {-1,0,1,2} | D. | {-2,-1,0,1,2} |
17.计算lg4+lg25=( )
| A. | 2 | B. | 3 | C. | 4 | D. | 10 |
4.设实数a,b满足|a|>|b|,则“a-b>0”是“a+b>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
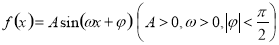 的图像过点
的图像过点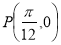 ,图像上与
,图像上与
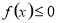 的取值范围
的取值范围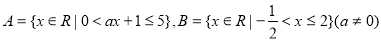 .
.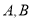 能否相等?若能,求出实数
能否相等?若能,求出实数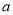 的值;若不能,试说明理由;
的值;若不能,试说明理由;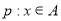 ,命题
,命题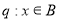 ,且
,且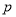 是
是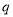 充分不必要条件,求实数
充分不必要条件,求实数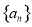 的前
的前 项和为
项和为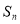 ,且
,且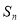
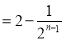 ,
,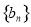 为等差数列,且
为等差数列,且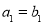 ,
,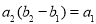 .
.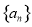 和
和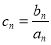 ,求数列
,求数列 的前
的前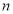 项和
项和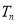 .
.