题目内容
设圆C与两圆(x+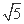 )2+y2=4,(x-
)2+y2=4,(x-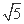 )2+y2=4中的一个内切,另一个外切.
)2+y2=4中的一个内切,另一个外切.
(1) 求圆C的圆心轨迹L的方程;
(2) 已知点M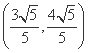 ,F(
,F(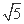 ,0),且点P为轨迹L上动点,求|MP-FP|的最大值及此时点P的坐标.
,0),且点P为轨迹L上动点,求|MP-FP|的最大值及此时点P的坐标.
(1) 两圆半径都为2,设圆C的半径为R,两圆心分别为F1(-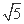 ,0),F2(
,0),F2(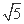 ,0).
,0).
由题意得R=CF1-2=CF2+2或R=CF2-2=CF1+2,
所以CF1-CF2=4<2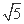 =F1F2.
=F1F2.
可知圆心C的轨迹是以F1,F2为焦点的双曲线,设方程为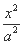 -
-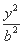 =1,则
=1,则
2a=4,a=2,c=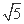 ,b2=c2-a2=1,b=1,
,b2=c2-a2=1,b=1,
所以轨迹L的方程为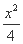 -y2=1.
-y2=1.
(2) 因为MP-FP≤MF=2,当且仅当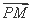 =λ
=λ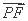 (λ>0)时,取“=”.
(λ>0)时,取“=”.
由kMF=-2知直线lMF:y=-2(x-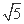 ),联立
),联立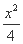 -y2=1并整理得15x2-32
-y2=1并整理得15x2-32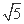 x+84=0,解得x=
x+84=0,解得x=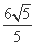 或x=
或x=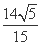 (舍去),此时P
(舍去),此时P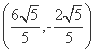 ,
,
所以MP-FP最大值等于2,此时P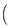
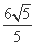 ,-
,-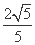
 .
.

练习册系列答案
相关题目
 ,2),则该椭圆的离心率为 .
,2),则该椭圆的离心率为 . 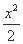 -
- =1的准线经过椭圆
=1的准线经过椭圆
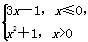 的函数值.其中需要用条件结构来描述算法的有( )
的函数值.其中需要用条件结构来描述算法的有( )