题目内容
已知函数y=3x2-ax+2a的图象与x轴相交于不同的两点A、B.
(1)若A、B两点分别在直线x=1的两侧,求实数a的取值范围;
(2)若A、B两点都在直线l:x=1的右侧,求实数a的取值范围.
(1)若A、B两点分别在直线x=1的两侧,求实数a的取值范围;
(2)若A、B两点都在直线l:x=1的右侧,求实数a的取值范围.
因为函数y=3x2-ax+2a的图象与x轴相交于不同的两点A、B,
所以△=a2-24a>0,即:a<0或a>24,…(3分).
且x1+x2=
,x1x2=
…(5分)
(1)若A、B两点分别在直线x=1的两侧,则有f(1)<0,…(7分)
即:3-a+2a<0,所以a<-3…(9分)
(2)若A、B两点都在直线x=1的右侧,设A(x1,0)、B(x2,0),则x1>1,x2>1
则有
,…(11分)解之得:a>6,…(13分).由△>0知,a>24…(14分)
所以△=a2-24a>0,即:a<0或a>24,…(3分).
且x1+x2=
| a |
| 3 |
| 2a |
| 3 |
(1)若A、B两点分别在直线x=1的两侧,则有f(1)<0,…(7分)
即:3-a+2a<0,所以a<-3…(9分)
(2)若A、B两点都在直线x=1的右侧,设A(x1,0)、B(x2,0),则x1>1,x2>1
则有
|

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
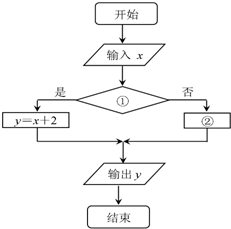 已知函数y=y=
已知函数y=y=