题目内容
已知函数y=
对定义域内的任意x的值都有-1≤f(x)≤4,则a的取值范围为
| ax+3 | x2+1 |
[-4,4]
[-4,4]
.分析:将已知条件转化为-1≤
≤4恒成立,
恒成立,令两个二次不等式的判别式小于等于0即得到答案.
| ax+3 |
| x2+1 |
|
解答:解:根据题意得:
-1≤
≤4恒成立,
所以
恒成立
所以
解得-4≤a≤4
故答案为[-4,4].
-1≤
| ax+3 |
| x2+1 |
所以
|
所以
|
解得-4≤a≤4
故答案为[-4,4].
点评:本题考查等价转化的能力及解决二次不等式恒成立常从二次项系数的符号及判别式来限制,属于基础题.

练习册系列答案
相关题目
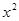 -ax-3(
-ax-3(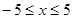 )
)