题目内容
已知数列 的前
的前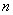 项和为
项和为 ,
, ,
, ,
, .
.
(Ⅰ) 求证:数列 是等比数列;
是等比数列;
(Ⅱ) 设数列 的前
的前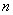 项和为
项和为 ,
, ,点
,点 在直线
在直线 上,若不等式
上,若不等式 对于
对于 恒成立,求实数
恒成立,求实数 的最大值.
的最大值.
解析:(Ⅰ)由 ,
,
得 ,
,
两式相减得 ,
,
所以 (
( ),
),
因为 ,所以
,所以 ,
, ,
,
所以 是以
是以 为首项,公比为
为首项,公比为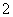 的等比数列
的等比数列
(Ⅱ)由(Ⅰ)得 ,因为点
,因为点 在直线
在直线 上,所以
上,所以 ,
,
故 是以
是以 为首项,
为首项, 为公差的等差数列,
为公差的等差数列,
则 ,所以
,所以 ,
,
当 时,
时, ,
,
因为 满足该式,所以
满足该式,所以
所以不等式 ,
,
即为 ,
,
令 ,则
,则 ,
,
两式相减得
 ,
,
所以
由 恒成立,即
恒成立,即 恒成立,
恒成立,
又 ,
,
故当 时,
时, 单调递减;当
单调递减;当 时,
时, ;
;
当 时,
时, 单调递增;当
单调递增;当 时,
时, ;
;
则 的最小值为
的最小值为 ,所以实数
,所以实数 的最大值是
的最大值是

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则复数
,则复数 ()
() B.
B. C.
C. D.
D.
 是首项为
是首项为 的等比数列,
的等比数列, 是其前
是其前 ,则数列
,则数列 前
前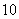 项和为( )
项和为( ) (B)
(B) (C)
(C) (D)
(D)
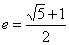 的双曲线
的双曲线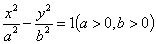 称为黄金双曲线.如图是双曲线
称为黄金双曲线.如图是双曲线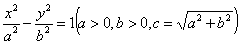 的图象,给出以下几个说法:
的图象,给出以下几个说法: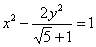 是黄金双曲线;
是黄金双曲线;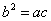 ,则该双曲线是黄金双曲线;
,则该双曲线是黄金双曲线;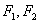 为左右焦点,
为左右焦点,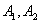 为左右顶点,
为左右顶点,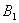 (0,
(0,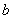 ),
),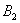 (0,﹣
(0,﹣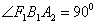 ,则该双曲线是黄金双曲线;
,则该双曲线是黄金双曲线;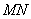 经过右焦点
经过右焦点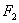 且
且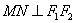 ,
,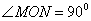 ,则该双曲线是黄金双曲线.
,则该双曲线是黄金双曲线.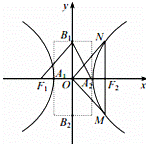
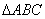 中,角
中,角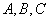 所对的边分别为
所对的边分别为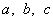 ,满足
,满足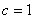 ,
,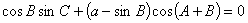 .
.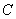 的大小;
的大小;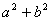 的最大值,并求取得最大值时角
的最大值,并求取得最大值时角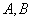 的值.
的值. ,
, ,
, ,则
,则 ( )
( ) (B)
(B) (C)
(C) (D)
(D)
 中,侧棱
中,侧棱 底面
底面 ,
, ,
, ,
, ,
, ,
, 是棱
是棱 中点.
中点.
 平面
平面 ;
; 是线段
是线段 上一动点,且
上一动点,且 ,当直线
,当直线 与平面
与平面 所成的角最大时,求
所成的角最大时,求 的值.
的值. 满足
满足 ,
, ,
, ,
, ,则
,则 的最小值为 .
的最小值为 .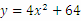 ,若欲使此设备的年平均花费最低,则此设备的使用年限x为
,若欲使此设备的年平均花费最低,则此设备的使用年限x为