题目内容
函数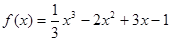 的单调递增区间为____________.
的单调递增区间为____________.
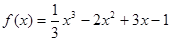 的单调递增区间为____________.
的单调递增区间为____________. 
本题考查导数知识的运用,考查函数的单调性,属于基础题
因为 ,那么根据导数的符号与单调性的关系可知,当
,那么根据导数的符号与单调性的关系可知,当 ,导数大于零,可知函数单调递增,故可知函数的单调递增区间为
,导数大于零,可知函数单调递增,故可知函数的单调递增区间为 。
。
解决该试题的关键是利用导数的符号与函数单调性的关系来判定。
因为
 ,那么根据导数的符号与单调性的关系可知,当
,那么根据导数的符号与单调性的关系可知,当 ,导数大于零,可知函数单调递增,故可知函数的单调递增区间为
,导数大于零,可知函数单调递增,故可知函数的单调递增区间为 。
。解决该试题的关键是利用导数的符号与函数单调性的关系来判定。

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 .(Ⅰ) 求
.(Ⅰ) 求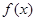 在
在 上的最小值;(Ⅱ) 若存在
上的最小值;(Ⅱ) 若存在 (
( 是常数,
是常数, )使不等式
)使不等式 成立,求实数
成立,求实数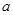 的取值范围;
的取值范围; 都有
都有 成立.
成立.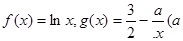 为实常数).
为实常数).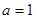 时,求函数
时,求函数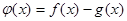 在
在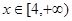 上的最小值;
上的最小值;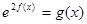 在区间
在区间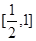 上有解,求实数
上有解,求实数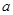 的取值范围;
的取值范围;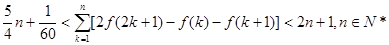
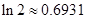 )
)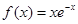 (x∈R).
(x∈R).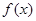 的单调区间和极值;
的单调区间和极值; 的图象与函数
的图象与函数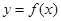 的图象关于直线x=1对称,证明当x>1时,
的图象关于直线x=1对称,证明当x>1时,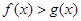 .
.  单调递减区间是
单调递减区间是 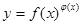 的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边取对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边取对数得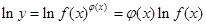 ,两边对
,两边对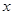 求导数,得
求导数,得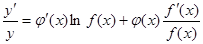 ,于是
,于是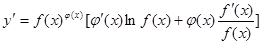 ,运用此方法可以求得函数
,运用此方法可以求得函数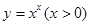 在
在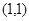 处的切线方程是________________.
处的切线方程是________________. 在
在 上是增函数,在
上是增函数,在 上是减函数.
上是减函数. 的解析式;
的解析式; 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,使得方程
,使得方程 在区间
在区间 上恰有两个相异实数根,若存在,求出
上恰有两个相异实数根,若存在,求出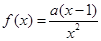 ,其中
,其中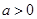 .
.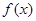 的单调区间;
的单调区间;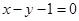 是曲线
是曲线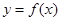 的切线,求实数
的切线,求实数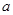 的值;
的值;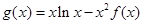 ,求
,求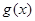 在区间
在区间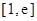 上的最大值.(其中
上的最大值.(其中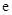 为自然对数的底数)
为自然对数的底数)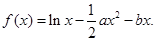
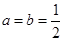 时,求函数
时,求函数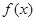 的最大值;
的最大值;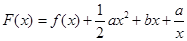 ,(
,(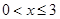 )其图象上任意一点
)其图象上任意一点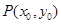 处切线的斜率
处切线的斜率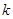 ≤
≤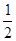 恒成立,求实数
恒成立,求实数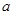 的取值范围;
的取值范围;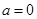 ,
,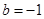 ,方程
,方程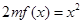 有唯一实数解,求正数
有唯一实数解,求正数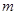 的值.
的值.