题目内容
5.已知数列{an}的前n项的和为Sn,且a1=1,a2=4,Sn+1=5Sn-4Sn-1(n≥2),等差数列{bn}满足b6=6,b9=12,(1)分别求出数列{an},{bn}的通项公式;
(2)若对于任意的n∈N*,(Sn+$\frac{1}{3}$)•k≥bn恒成立,求实数k的取值范围.
分析 (1)由an=Sn-Sn-1,可得an+1=4an,即有数列{an}为首项为1,公比为4的等比数列,运用等比数列的通项公式可得an,再由等差数列的通项公式可得d=2,进而得到{bn}的通项公式;
(2)运用等比数列的求和公式,可得$\frac{1}{3}$k≥$\frac{2n-6}{{4}^{n}}$的最大值,令cn=$\frac{2n-6}{{4}^{n}}$,判断单调性,可得最大值,解不等式可得k的范围.
解答 解:(1)Sn+1=5Sn-4Sn-1(n≥2),可得
Sn+1-Sn=4(Sn-Sn-1)(n≥2),
即为an+1=4an,
则数列{an}为首项为1,公比为4的等比数列,
则an=4n-1;
等差数列{bn}满足b6=6,b9=12,
设公差为d,可得3d=b9-b6=6,
解得d=2,即有bn=b6+(n-6)d=2n-6.
(2)对于任意的n∈N*,(Sn+$\frac{1}{3}$)•k≥bn恒成立,
即有($\frac{1-{4}^{n}}{1-4}$+$\frac{1}{3}$)•k≥2n-6,
可得$\frac{1}{3}$k≥$\frac{2n-6}{{4}^{n}}$的最大值,
令cn=$\frac{2n-6}{{4}^{n}}$,
由cn+1-cn=$\frac{2(n+1)-6}{{4}^{n+1}}$-$\frac{2n-6}{{4}^{n}}$=$\frac{20-6n}{{4}^{n}}$,
当1≤n≤4时,数列{cn}递增;
当n≥4时,数列{cn}递减.
可得c4为最大值,且为$\frac{1}{128}$,
即有$\frac{1}{3}$k≥$\frac{1}{128}$,
解得k≥$\frac{3}{128}$.
点评 本题考查等差数列和等比数列的通项公式的运用,注意数列的通项和前n项和的关系,考查数列不等式恒成立的求法,注意运用数列的单调性,考查运算能力,属于中档题.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案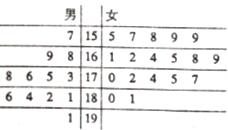 某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试跳远的成绩用茎叶图表示如下(单位:cm):
某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试跳远的成绩用茎叶图表示如下(单位:cm):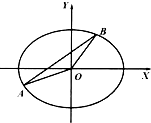 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,不经过原点O的直线l:y=kx+m(k>0)与椭圆E相交于不同的两点A、B,直线OA,AB,OB的斜率依次构成等比数列.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,不经过原点O的直线l:y=kx+m(k>0)与椭圆E相交于不同的两点A、B,直线OA,AB,OB的斜率依次构成等比数列. 如图,在三棱柱ABC-A1B1C1中,G为ABC的重心,延长线段AG交BC于F,B1F交BC1于E.
如图,在三棱柱ABC-A1B1C1中,G为ABC的重心,延长线段AG交BC于F,B1F交BC1于E.