题目内容
已知定点A(a,0)和椭圆x2+2y2=8上的动点P(x,y)
(1)a=2且|PA|=
,计算点P的坐标;
(2)若0<a<3且|PA|的最小值为1,求实数a的值.
(1)a=2且|PA|=
3
| ||
| 2 |
(2)若0<a<3且|PA|的最小值为1,求实数a的值.
分析:(1)根据a=2,得A点的坐标,从而得到|PA|=
=
,再结合椭圆的方程x2+2y2=8联解可得x=1或7(其中x=7>2
不合题意舍去),回代到方程组中可以求出y的值,从而得出点P的坐标;
(2)设P点坐标为(x,y),可得|PA|2=(x-a)2+y2,再根据椭圆方程得到y2=4-
代入上式,得关于x的二次函数g(x)=
x2-2ax+a2+4,再讨论它的对称轴x=2a与3的大小关系,得到g(x)在区间[- 2
,2
]的最小值的两种不同情况,进行分类讨论,最后解关于a的方程,综合可得实数a的值.
| (x-2)2+y2 |
3
| ||
| 2 |
| 2 |
(2)设P点坐标为(x,y),可得|PA|2=(x-a)2+y2,再根据椭圆方程得到y2=4-
| x2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
解答:解:(1)若a=2,则A(2,0),设P点坐标为(x,y),
由|PA|=
,可得(x-2)2+y2=
…①…(3分)
∴
,消去y得x2-8x+7=0,
解之得x=1或7,其中x=7>2
不合题意舍去.…(5分)
将x=1代入①,解得
,
所以点P的坐标为(1, ±
)…(7分)
(2)设P点坐标为(x,y),可得|PA|2=(x-a)2+y2
将y2=4-
代入上式,
得|PA|2=
x2-2ax+a2+4(其中- 2
≤x≤2
)…(9分)
令g(x)=
x2-2ax+a2+4,
g(x)是一个二次函数,其对称轴方程为x=2a
①若0<2a<2
,即0<a<
,
则g(x)min=g(2a)=4-a2=1,
解得a=±
(舍去)…(11分)
②若2
≤2a<6,即
≤a<3,
则g(x)min=g(2
)=8-4
a+a2=1,
解得a=2
±1,其中a=2
+1不合题意,舍去.
所以a=2
-1…(13分)
综上可知,a=2
-1.…(14分)
由|PA|=
3
| ||
| 2 |
| 9 |
| 2 |
∴
|
解之得x=1或7,其中x=7>2
| 2 |
将x=1代入①,解得
|
所以点P的坐标为(1, ±
| ||
| 2 |
(2)设P点坐标为(x,y),可得|PA|2=(x-a)2+y2
将y2=4-
| x2 |
| 2 |
得|PA|2=
| 1 |
| 2 |
| 2 |
| 2 |
令g(x)=
| 1 |
| 2 |
g(x)是一个二次函数,其对称轴方程为x=2a
①若0<2a<2
| 2 |
| 2 |
则g(x)min=g(2a)=4-a2=1,
解得a=±
| 3 |
②若2
| 2 |
| 2 |
则g(x)min=g(2
| 2 |
| 2 |
解得a=2
| 2 |
| 2 |
所以a=2
| 2 |
综上可知,a=2
| 2 |
点评:本题对圆锥曲线中的距离计算和距离的最小值的问题加以研究,着重考查了椭圆的标准方程和二次函数求闭区间上的最值等知识点,属于中档题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 已知定点A(-2,0),B(2,0),及定点F(1,0),定直线l:x=4,不在x轴上的动点M到定点F的距离是它到定直线l的距离的
已知定点A(-2,0),B(2,0),及定点F(1,0),定直线l:x=4,不在x轴上的动点M到定点F的距离是它到定直线l的距离的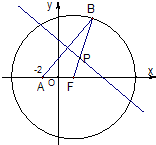 已知定点A(-2,0),动点B是圆F:(x-2)2+y2=64(F为圆心)上一点,线段AB的垂直平分线交BF于P.
已知定点A(-2,0),动点B是圆F:(x-2)2+y2=64(F为圆心)上一点,线段AB的垂直平分线交BF于P.