题目内容
已知定点A(12,0),M为曲线(x-6)2+y2=4上的动点,
(1)若
= 2
,试求动点P的轨迹C的方程
(2)若直线l:y=-x+a与曲线C相交与不同的两点E,F.O为坐标原点,且
•
=12,实数a的值.
(1)若
| AP |
| AM |
(2)若直线l:y=-x+a与曲线C相交与不同的两点E,F.O为坐标原点,且
| OE |
| OF |
分析:设P(x,y),M (a,b)
(1)由
=2
可得a,b与x,y之间的关系,结合M(a,b)为为曲线(x-6)2+y2=4上的点可求x,y的关系,即可求曲线C 的方程
(2)联立直线y=-x+a与曲线C的方程,设E(x1,y1),F(x2,y2),方程的根与系数关系可求x1+x2,x1x2,结合y1y2=(a-x1)(a-x2)=a2-a(x1+x2)+x1x2=
及
•
=x1x2+y1y2,代入可求a
(1)由
| AP |
| AM |
(2)联立直线y=-x+a与曲线C的方程,设E(x1,y1),F(x2,y2),方程的根与系数关系可求x1+x2,x1x2,结合y1y2=(a-x1)(a-x2)=a2-a(x1+x2)+x1x2=
| a2-16 |
| 2 |
| OE |
| OF |
解答:解:设P(x,y),M (a,b)
(1)
=(x-12,y),
=(a-12,b)
∵
=2
∴
∴
∵M(a,b)为为曲线(x-6)2+y2=4上的点
∴(a-6)2+b2=4上
∴
2+
=4,即动点C的轨迹方程为x2+y2=16
(2)联立方程
可得2x2-2ax+a2-16=0
设E(x1,y1),F(x2,y2),
则x1+x2=a,x1x2=
∴y1y2=(a-x1)(a-x2)=a2-a(x1+x2)+x1x2=
∴
•
=x1x2+y1y2=a2-16=12
∴a2=28
∴a=±2
(1)
| AP |
| AM |
∵
| AP |
| AM |
∴
|
∴
|
∵M(a,b)为为曲线(x-6)2+y2=4上的点
∴(a-6)2+b2=4上
∴
| x |
| 4 |
| y2 |
| 4 |
(2)联立方程
|
设E(x1,y1),F(x2,y2),
则x1+x2=a,x1x2=
| a2-16 |
| 2 |
∴y1y2=(a-x1)(a-x2)=a2-a(x1+x2)+x1x2=
| a2-16 |
| 2 |
∴
| OE |
| OF |
∴a2=28
∴a=±2
| 7 |
点评:本题考查利用相关点法求解点的轨迹方程,直线与曲线相交关系的应用,方程的根与系数关系的应用,向量的数量积的坐标表示等综合应用

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
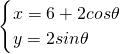 上的动点.
上的动点.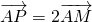 ,试求动点P的轨迹C的方程;
,试求动点P的轨迹C的方程;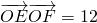 ,求∠EOF的余弦值和实数a的值.
,求∠EOF的余弦值和实数a的值.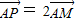 ,试求动点P的轨迹C的方程
,试求动点P的轨迹C的方程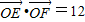 ,实数a的值.
,实数a的值.