题目内容
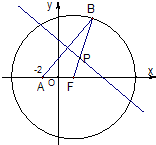 已知定点A(-2,0),动点B是圆F:(x-2)2+y2=64(F为圆心)上一点,线段AB的垂直平分线交BF于P.
已知定点A(-2,0),动点B是圆F:(x-2)2+y2=64(F为圆心)上一点,线段AB的垂直平分线交BF于P.(Ⅰ)求动点P的轨迹方程;
(Ⅱ)是否存在过点E(0,-4)的直线l交P点的轨迹于点R,T,且满足
| OR |
| OT |
| 16 |
| 7 |
分析:(I)由题意得|PA|=|PB|且|PB|+|PF|=r=8.故|PA|+|PF|=8>|AF|=4∴P点轨迹为以A、F为焦点的椭圆,从而动点P的轨迹方程;
(II)假设存在满足题意的直线L,设直线L的斜率为k,R(x1,y1),T(x2,y2).∵
•
=
,∴x1x2+y1y2=
.从而求得直线方程.
(II)假设存在满足题意的直线L,设直线L的斜率为k,R(x1,y1),T(x2,y2).∵
| OR |
| OT |
| 16 |
| 7 |
| 16 |
| 7 |
解答:解:(I)由题意得|PA|=|PB|且|PB|+|PF|=r=8.故|PA|+|PF|=8>|AF|=4
∴P点轨迹为以A、F为焦点的椭圆.
设椭圆方程为
+
=1(a>b>0)
∴p点轨迹方程为
+
=1.
(II)假设存在满足题意的直线L.易知当直线的斜率不存在时,
•
<0不满足题意.
故设直线L的斜率为k,R(x1,y1),T(x2,y2).
∵
•
=
,∴x1x2+y1y2=
.
由
得(3+4k2)x2-32kx+16=0.由△>0得,(-32k)2-4(3+4k2)•16>0解得k2>
.…①.
∴x1+x2=
,x1•x2=
.
∴y1•y2=(kx1-4)(kx2-4)=k2x1x2-4k(x1+x2)+16,
故x1x2+y1y2=
+
-
+16=
.解得k2=1.…②.
由①、②解得k=±1.
∴直线l的方程为y=±x-4.
故存在直线l:,x+y+4=0或x-y-4=0,满足题意.
∴P点轨迹为以A、F为焦点的椭圆.
设椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
∴p点轨迹方程为
| x2 |
| 16 |
| y2 |
| 12 |
(II)假设存在满足题意的直线L.易知当直线的斜率不存在时,
| OR |
| OT |
故设直线L的斜率为k,R(x1,y1),T(x2,y2).
∵
| OR |
| OT |
| 16 |
| 7 |
| 16 |
| 7 |
由
|
| 1 |
| 4 |
∴x1+x2=
| 32k |
| 3+4k2 |
| 16 |
| 3+4k2 |
∴y1•y2=(kx1-4)(kx2-4)=k2x1x2-4k(x1+x2)+16,
故x1x2+y1y2=
| 16 |
| 3+4k2 |
| 16k2 |
| 3+4k2 |
| 128k2 |
| 3+4k2 |
| 16 |
| 7 |
由①、②解得k=±1.
∴直线l的方程为y=±x-4.
故存在直线l:,x+y+4=0或x-y-4=0,满足题意.
点评:本题考查椭圆定义的运用及待定系数法求椭圆方程;(II)关键是将条件等价变形,同时应注意分类讨论.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
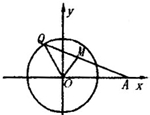 如图,已知定点A(2,0),点Q是圆x2+y2=1上的动点,∠AOQ的平分线交AQ于M,当Q点在圆上移动时,求动点M的轨迹方程.
如图,已知定点A(2,0),点Q是圆x2+y2=1上的动点,∠AOQ的平分线交AQ于M,当Q点在圆上移动时,求动点M的轨迹方程.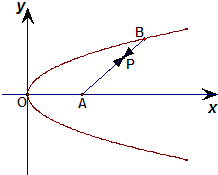 如图,已知定点A(2,0)及抛物线y2=x,点B在该抛物线上,若动点P使得
如图,已知定点A(2,0)及抛物线y2=x,点B在该抛物线上,若动点P使得