题目内容
已知二面角αlβ为60°,AB⊂α,AB⊥l,A为垂足,CD⊂β,C∈l,∠ACD=135°,则异面直线AB与CD所成角的余弦值为( )
A.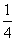 B.
B.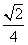
C.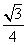 D.
D.
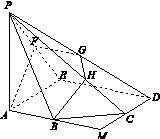
B [解析] 如图所示,在平面α内过点C作CF∥AB,过点F作FE⊥β,垂足为点E,连接CE,则CE⊥l,所以∠ECF=60°.过点E作DE⊥CE,交CD于点D1,连接FD1.不妨设FC=2a,则CE=a,EF= a.因为∠ACD=135°,所以∠DCE=45°,所以,在Rt△DCE中,D1E=CE=a,CD1=
a.因为∠ACD=135°,所以∠DCE=45°,所以,在Rt△DCE中,D1E=CE=a,CD1= a,∴FD1=2a,∴cos∠DCF=
a,∴FD1=2a,∴cos∠DCF= =
=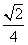 .
.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 B.16π C.9π D.
B.16π C.9π D.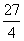
 B.
B.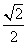
 ﹣x2=1,点A的坐标为(0,﹣
﹣x2=1,点A的坐标为(0,﹣ ),B是圆(x﹣
),B是圆(x﹣