题目内容
如图,在半径为30 cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A,B在直径上,点C,D在圆周上.

(1)怎样截取才能使截得的矩形ABCD的面积最大?并求最大面积.
(2)若将所截得的矩形铝皮 ABCD卷成一个以AD为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),应怎样截取,才能使做出的圆柱形罐子体积最大
ABCD卷成一个以AD为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),应怎样截取,才能使做出的圆柱形罐子体积最大 ?并求最大体积.
?并求最大体积.
(1)(法一)连接OC.
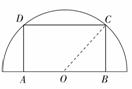
设BC=x,矩形ABCD的面积为S,
则AB=2 ,其中0<x<30.
,其中0<x<30.
所以S=2x
 =2
=2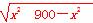 ≤x2+(900-x2)=900,
≤x2+(900-x2)=900,
当且仅当x2=900-x2,即x=15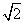 时,S取得最大值为900 cm2.
时,S取得最大值为900 cm2.
(法二)连接OC.设∠BOC=θ,矩形ABCD的面积为S,
则BC=30sin θ,OB=30 cos θ,其中0<θ<
cos θ,其中0<θ< .
.
所以S=AB·BC=2OB·BC=900 sin 2θ.
当sin 2θ=1,即θ=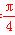 时,
时,
S取最大值为900 cm2,此时BC=15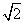 .
.
所以取BC为15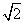 cm时,矩形ABCD的面积最大,最大值为900 cm2.
cm时,矩形ABCD的面积最大,最大值为900 cm2.
(2)(法一)设圆柱底面半径为r,高为x,体积为V,
由AB=2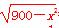 =2πr,得r=
=2πr,得r=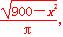 ,
,
所以V=πr2 h=
h= (900x-x3),其中0<x<30.
(900x-x3),其中0<x<30.
由V′= (900-3x2)=0,得x=10
(900-3x2)=0,得x=10 ,
,
因此V= (900x-x3)在(0,10
(900x-x3)在(0,10 )上是增函数,在(10
)上是增函数,在(10 ,30)上是减函数.
,30)上是减函数.
所以当BC=10 时,V取得最大值为
时,V取得最大值为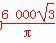 cm3.
cm3.
(法二)连接OC.设∠BOC=θ,圆柱底面半径为r,高为h,体积为V,则圆柱的底面半径为r= ,高h=30sin θ,其中0<θ<
,高h=30sin θ,其中0<θ<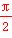 .
.
所以V=πr2h= sin θcos2θ
sin θcos2θ
= (sin θ-sin3θ).
(sin θ-sin3θ).
设t=sin θ(0<t<1),则V= (t-t3).
(t-t3).
由V′= (1-3t2)=0,得t=
(1-3t2)=0,得t=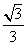 .
.
因此V= (t-t3)在
(t-t3)在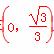 上是增函数,在
上是增函数,在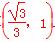 上是减函数,
上是减函数,
所以当t=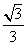 ,即sin θ=
,即sin θ=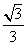 ,BC=10
,BC=10 时,V取得最大值为
时,V取得最大值为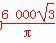 cm3.
cm3.
所以取BC为10 cm时,做出的圆柱形罐子体积最大,最大值为
cm时,做出的圆柱形罐子体积最大,最大值为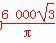 cm3.
cm3.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案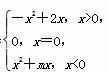 是奇函数.
是奇函数.
 B.a<0,4a+b=0
B.a<0,4a+b=0 -
-
 -(
-(
 -1)0=( )
-1)0=( ) C.-45 D.-40
C.-45 D.-40 3
3 B.
B. C.
C. D.
D.