题目内容
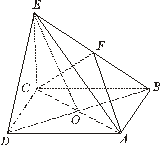
在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.
(Ⅰ) 求证:DE∥平面ACF;
(Ⅱ)若AB=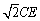 ,在线段EO上是否存在点G,使CG⊥平面BDE?若存在,求出
,在线段EO上是否存在点G,使CG⊥平面BDE?若存在,求出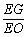 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 |
解析(Ⅰ)证明:连接OF.
由四边形ABCD是正方形可知,点O为BD的中点.
又F为BE的中点,所以OF ∥DE.
又OF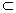 平面ACF,DE
平面ACF,DE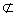 平面ACF,
平面ACF,
所以DE∥平面ACF.
(Ⅱ)解法一:若CG⊥平面BDE,则必有CG⊥OE,
于是作CG⊥OE于点G.
由EC⊥底面ABCD,所以BD⊥EC,又底面ABCD是正方形,
所以BD⊥AC,又EC∩AC=C,所以BD⊥平面ACE.分
而CG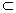 平面ACE,所以CG⊥BD.
平面ACE,所以CG⊥BD.
又OE∩BD=O,所以CG⊥平面BDE.
又AB=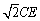 ,所以
,所以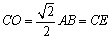 ,
,
所以G为EO的中点,所以 .
.
解法二:取EO的中点G,连接CG.在四棱锥E—ABCD中,
AB=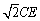 ,
,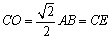 ,所以CG⊥EO.
,所以CG⊥EO.
又由EC⊥底面ABCD,BD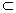 底面ABCD,所以EC⊥BD,
底面ABCD,所以EC⊥BD,
由四边形ABCD是正方形可知,AC⊥BD,
又AC∩EC=C,
所以BD⊥平面ACE,
而BD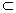 平面BDE,
平面BDE,
所以,平面ACE⊥平面BDE,且平面ACE∩平面BDE=EO,
因为CG⊥EO,CG  平面ACE,所以CG⊥平面BDE,
平面ACE,所以CG⊥平面BDE,
故在线段EO上存在点G,使CG⊥平面BDE.
由G为EO的中点,得 .
.

练习册系列答案
相关题目

 的值域为 .
的值域为 . 中,
中, 是自变量,
是自变量, 是常数.当
是常数.当 中取不同的值时,所得五个函数的图像都要经过的一个定点坐标是________.
中取不同的值时,所得五个函数的图像都要经过的一个定点坐标是________.
 (B)
(B) (C)
(C) (D)
(D)

 ,则A所表示的平面区域(不含边界的阴影部分)是( )
,则A所表示的平面区域(不含边界的阴影部分)是( )



 , 则a 5 =
, 则a 5 =  ,则
,则 _________________ .
_________________ .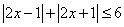 的解集为__________.
的解集为__________.