题目内容
在一个花瓶中装有6枝鲜花,其中3枝山茶花,2枝杜鹃花和1枝君子兰,从中任取2枝鲜花.
(Ⅰ)求恰有一枝山茶花的概率;
(Ⅱ)求没有君子兰的概率.
解:设3枝山茶花为a、b、c,2枝杜鹃花为m、n,1枝君子兰为d. 则从6枝鲜花中任取2枝的基本事件有: (a,b)、(a,c)、(a,d)、(a,m)、(a,n)、(b,c)、(b,d)、(b,m)、(b,n)、(c,d)、(c,m)、(c,n)、(d,m)、(d,n)、(m,n) 共15种.
(Ⅰ)其中恰有一枝山茶花的基本事件有: (a,d)、(a,m)、(a,n)、(b,d)、(b,m)、(b,n)、(c,d)、(c,m)、(c,n)共9种.所以恰有一枝山茶花的概率为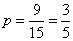 .
.
(Ⅱ)其中没有君子兰的基本事件有:(a,b)、(a,c)、(a,m)、(a,n)、(b,c)、(b,m)、(b,n)、(c,m)、(c,n)、(m,n) 共10种.所以没有君子兰的概率为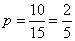 .················· 1
.················· 1

练习册系列答案
相关题目
 的两条渐近线与直线
的两条渐近线与直线 分别交于
分别交于 两点,
两点, 为该双曲线的右焦点.若
为该双曲线的右焦点.若 , 则该双曲线的离心率的取值范围是
, 则该双曲线的离心率的取值范围是 B.
B. C.
C. D.
D.
 ,
, 与
与 (
( )的大致图像正确的是
)的大致图像正确的是
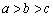 (B)
(B)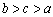 (C)
(C)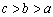 (D)
(D)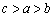


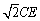 ,在线段EO上是否存在点G,使CG⊥平面BDE?若存在,求出
,在线段EO上是否存在点G,使CG⊥平面BDE?若存在,求出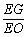 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.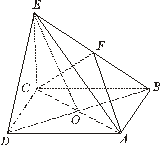

 的反函数
的反函数 _____________.
_____________.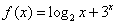 ,正实数
,正实数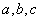 成公差为正数的等差数列,且满足
成公差为正数的等差数列,且满足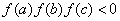 ,且实数
,且实数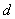 是函数
是函数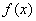 的一个零点。给出下列四个不等式:其中有可能成立的不等式有( )①
的一个零点。给出下列四个不等式:其中有可能成立的不等式有( )①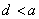 ;②
;②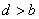 ;③
;③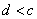 ;④
;④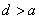 .
.