题目内容
已知△ABC中,内角A,B,C的对边分别为a,b,c,其中a=2,c=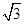 .
.
(1)若sinC=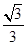 ,求sinA的值;
,求sinA的值;
(2)设f(C)=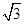 sinCcosC-cos2C,求f(C)的取值范围.
sinCcosC-cos2C,求f(C)的取值范围.
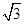 .
.(1)若sinC=
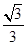 ,求sinA的值;
,求sinA的值;(2)设f(C)=
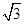 sinCcosC-cos2C,求f(C)的取值范围.
sinCcosC-cos2C,求f(C)的取值范围.(1) (2)(-1,
(2)(-1, ]
]
 (2)(-1,
(2)(-1, ]
]解:(1)由正弦定理得 =
= ,
,
∴sinA= =
= =
= .
.
(2)在△ABC中,由余弦定理,得c2=b2+a2-2bacosC,
∴3=b2+4-4bcosC,即b2-4cosC·b+1=0,由题知关于b的一元二次方程应该有解,
令Δ=(4cosC)2-4≥0,得cosC≤- (舍去)或cosC≥
(舍去)或cosC≥ ,
,
∴0<C≤ .
.
∴f(C)= sin2C-
sin2C- =sin(2C-
=sin(2C- )-
)- (-
(- <2C-
<2C- ≤
≤ ),
),
∴-1<f(C)≤ .
.
故f(C)的取值范围为(-1, ].
].
 =
= ,
,∴sinA=
 =
= =
= .
.(2)在△ABC中,由余弦定理,得c2=b2+a2-2bacosC,
∴3=b2+4-4bcosC,即b2-4cosC·b+1=0,由题知关于b的一元二次方程应该有解,
令Δ=(4cosC)2-4≥0,得cosC≤-
 (舍去)或cosC≥
(舍去)或cosC≥ ,
,∴0<C≤
 .
.∴f(C)=
 sin2C-
sin2C- =sin(2C-
=sin(2C- )-
)- (-
(- <2C-
<2C- ≤
≤ ),
),∴-1<f(C)≤
 .
.故f(C)的取值范围为(-1,
 ].
].
练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 ,∠A、∠B、∠C的大小成等差数列,且
,∠A、∠B、∠C的大小成等差数列,且
 ,求∠A的大小;
,求∠A的大小; 中,角
中,角 、
、 、
、 所对应的边分别为
所对应的边分别为 、
、 、
、 ,已知
,已知 ,则
,则 .
. 中,角
中,角 所对的边分别为
所对的边分别为 ,若
,若 ,且
,且 ,则下列关系一定不成立的是( ).
,则下列关系一定不成立的是( ).



 ,AC=2
,AC=2 ,cosC=
,cosC= .
.
 或
或 B.
B. 或
或 D.
D. ,
, ,
, ,则
,则 ( )
( )



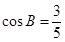 .
.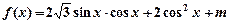 在区间
在区间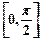 上的最大值为2
上的最大值为2 .
.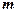 的值;
的值;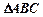 中的角
中的角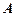 ,
,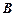 ,
,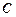 所对的边是
所对的边是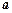 ,
,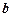 ,
,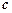 ,若
,若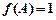
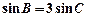 ,
,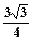 . 求边长
. 求边长