题目内容
已知函数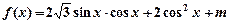 在区间
在区间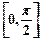 上的最大值为2
上的最大值为2 .
.
(1)求常数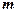 的值;
的值;
(2)在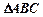 中的角
中的角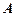 ,
,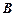 ,
,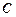 所对的边是
所对的边是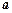 ,
,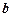 ,
,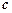 ,若
,若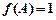
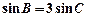 ,
,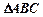 面积为
面积为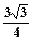 . 求边长
. 求边长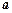 .
.
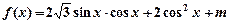 在区间
在区间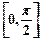 上的最大值为2
上的最大值为2 .
.(1)求常数
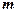 的值;
的值;(2)在
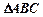 中的角
中的角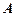 ,
,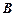 ,
,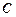 所对的边是
所对的边是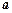 ,
,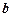 ,
,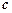 ,若
,若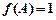
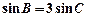 ,
,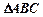 面积为
面积为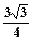 . 求边长
. 求边长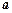 .
.(1) (2)
(2)
 (2)
(2)
解:(1)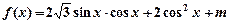



∵ ∴
∴
∵ 函数 在区间
在区间 上是增函数,在区间
上是增函数,在区间 上是减函数 ∴当
上是减函数 ∴当 即
即 时,函数
时,函数 在区间
在区间 上取到最大值.
上取到最大值.
此时, 得
得
(2)∵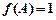 ∴
∴  ∴
∴  ,解得
,解得 (舍去)或
(舍去)或 ∵
∵ 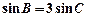 ,
, ∴
∴  …………①
…………①
∵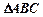 面积为
面积为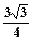
∴ 即
即 …………②
…………②
由①和②解得
∵
∴
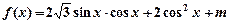



∵
 ∴
∴
∵ 函数
 在区间
在区间 上是增函数,在区间
上是增函数,在区间 上是减函数 ∴当
上是减函数 ∴当 即
即 时,函数
时,函数 在区间
在区间 上取到最大值.
上取到最大值.此时,
 得
得
(2)∵
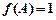 ∴
∴  ∴
∴  ,解得
,解得 (舍去)或
(舍去)或 ∵
∵ 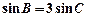 ,
, ∴
∴  …………①
…………①∵
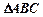 面积为
面积为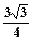
∴
 即
即 …………②
…………②由①和②解得

∵

∴


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
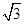 .
.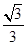 ,求sinA的值;
,求sinA的值;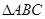 中,已知
中,已知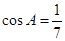 ,
,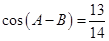 且
且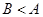 .
.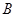 和
和 的值;
的值;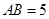 ,求边
,求边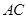 的长.
的长.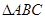 的内角
的内角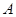 、
、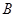 、
、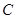 所对的边分别为
所对的边分别为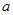 ,
,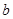 ,
,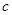 .若
.若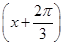 +2cos2
+2cos2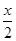 ,x∈R.
,x∈R.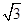 ,求a的值.
,求a的值.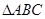 中,a,b,c分别是内角A,B,C所对的边,
中,a,b,c分别是内角A,B,C所对的边,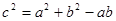 .
. 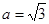 ,
,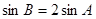 ,求
,求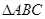 中,角
中,角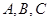 所对的边分别为
所对的边分别为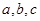 ,且
,且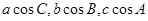 成等差数列.
成等差数列.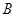 的大小;
的大小;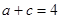 ,求
,求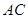 边上中线长的最小值.
边上中线长的最小值.
 中,若
中,若 ,
, ,
, ,则
,则 .
.