题目内容
已知数列{an}的相邻两项an,an+1是关于x 的方程x2-2n x+ bn=0 (n∈N*)的两根,且a1=1.
(1)求数列{ an}和{bn}的通项公式;
(2)设Sn是数列{an}的前n项的和,问是否存在常数λ,使得bn-λSn>0对任意n∈N*都成立,若存在,求出λ的取值范围;若不存在,请说明理由.
(1)证法1:∵an,an+1是关于x 的方程x2-2n x+ bn=0 (n∈N*)的两根,
∴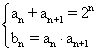
由an+an+1=2n,得 ,故数列
,故数列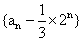
是首项为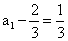 ,公比为-1的等比数列.
,公比为-1的等比数列.
证法2:∵an,an+1是关于x 的方程x2-2n x+ bn=0 (n∈N*)的两根,
∴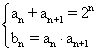
∵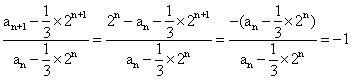 ,
,
故数列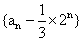 是首项为
是首项为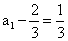 ,公比为-1的等比数列.
,公比为-1的等比数列.
(2)解:由(1)得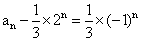 ,即
,即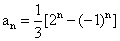 ,
,
∴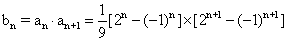

∴Sn=a1+ a2+ a3+…+ an=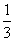 [(2+22+23+…+2n)-[(-1)+ (-1)2+…+(-1)n]
[(2+22+23+…+2n)-[(-1)+ (-1)2+…+(-1)n]
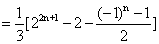 ,
,
要使得bn-λSn>0对任意n∈N*都成立,
即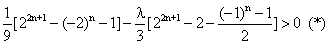 对任意n∈N*都成立.
对任意n∈N*都成立.
①当n为正奇数时,由(*)式得 ,
,
即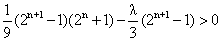 ,
,
∵2n+1-1>0,∴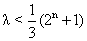 对任意正奇数n都成立.
对任意正奇数n都成立.
当且仅当n=1时,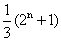 有最小值1,∴λ<1.
有最小值1,∴λ<1.
①当n为正奇数时,由(*)式得 ,
,
即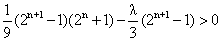 ,
,
∵2n+1-1>0,∴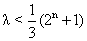 对任意正奇数n都成立.
对任意正奇数n都成立.
当且仅当n=1时,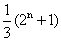 有最小值1,∴λ<1.
有最小值1,∴λ<1.
②当n为正偶数时,由(*)式得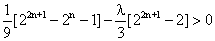 ,
,
即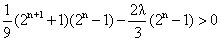 ,
,
∵2n-1>0,∴ 对任意正偶数n都成立.
对任意正偶数n都成立.
当且仅当n=2时,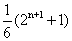 有最小值1.5,∴λ<1.5.
有最小值1.5,∴λ<1.5.
综上所述,存在常数λ,使得bn-λSn>0对任意n∈N*都成立,λ的取值范围是(-∞,1).

 那么
那么 的值为 .
的值为 . 的定义域是 .
的定义域是 . B.
B. C.
C. D.
D.
 在两直线
在两直线 和
和 之间的带状区域内(含边界),则
之间的带状区域内(含边界),则
 的最小值为_________
的最小值为_________ 与直线x=1,x=4及x轴所围成的区域的面积是( )
与直线x=1,x=4及x轴所围成的区域的面积是( ) B.ln2 C.2ln2 D.ln2-2
B.ln2 C.2ln2 D.ln2-2 ( )
( ) 上单调递增 B.在
上单调递增 B.在 上单调递增,在
上单调递增,在 上单调递减
上单调递减 上单调递减 D.在
上单调递减 D.在 上单调递减,在
上单调递减,在 上单调递增
上单调递增 的解集是
的解集是  B.
B. C.
C. D.
D.
 表示的平面区域为
表示的平面区域为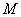 ,不等式
,不等式 表示的平面区域为
表示的平面区域为 .现随机向区域
.现随机向区域