题目内容
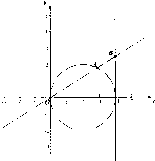
在圆（x-2）2+（y-2）2=8内有一平面区域E：
，点P是圆内的任意一点，而且出现任何一个点是等可能的．若使点P落在平面区域E内的概率最大，则m=
|
0
0
．分析：分别求出不等式组
表示的平面区域为E，判断E的面积最大时m的值，根据几何概型概率计算方法，求得m．
|
解答：解：如图阴影部分表示区域E，点P落在平面区域E内的概率=
，
当m=0时，区域E的面积最大，故使点P落在平面区域E内的概率最大，
故答案是0．
| E的面积 |
| 圆的面积 |
当m=0时，区域E的面积最大，故使点P落在平面区域E内的概率最大，
故答案是0．
点评：本题考查几何概型，考查线性规划的知识．
练习册系列答案
阅读快车系列答案
相关题目
已知点B（
，0），点O为坐标原点，点A在圆（x-
）2+（y-
）2=1上，则向量
与
的夹角θ的最大值与最小值分别为（ ）
| 2 |
| 2 |
| 2 |
| OA |
| OB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知点A（x1，y1）在圆（x-2）2+y2=4上运动，点A不与（0，0）重合，点B（4，y0）在直线x=4上运动，动点M（x，y）满足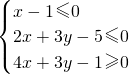
，点Q（x，y）在圆（x+2）2+（y+2）2=1上，则|PQ|的最大值与最小值为