题目内容
已知定义域为R的函数 (a、b∈R)有最大值和最小值,且最大值与最小值的和为6,则3a-2b= ( )
(a、b∈R)有最大值和最小值,且最大值与最小值的和为6,则3a-2b= ( )
A.7 B.8 C.9 D.1
C
【解析】
试题分析:由已知得∵函数y=f(x)=a+ =a+bx+
=a+bx+
有最大值和最小值,
∴必有b=0,y=f(x)=a+ ,即y-a=
,即y-a= .
.
∴3sinx+(a-y)cosx=2y-2a,∴ sin(x+φ)=2y-2a.
sin(x+φ)=2y-2a.
再根据|sin(x+φ)|=| |≤1,可得
|≤1,可得 ,故有a-
,故有a- ≤y≤a+
≤y≤a+ .
.
再根据最大值与最小值之和为6,可得2a=6,即a=3
考点:本题考查三角函数的最值

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 ,则该三棱锥外接球的表面积为____.
,则该三棱锥外接球的表面积为____. ,点E、F分别为棱AB、PD的中点.
,点E、F分别为棱AB、PD的中点.
 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 :
: 的焦点为
的焦点为 ,准线为
,准线为 ,
, 是
是 上一点,
上一点, 是直线
是直线 与
与 ,则
,则 = .
= . 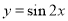 的图像向右平移
的图像向右平移 个单位,再向上平移1个单位,所得函数图像对应的解析式为( )
个单位,再向上平移1个单位,所得函数图像对应的解析式为( )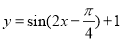 B.
B.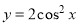
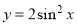 D.
D.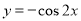
 是
是 的内接四边形,
的内接四边形, 的延长线与
的延长线与 的延长线交于点
的延长线交于点 ,且
,且 .
.
 ;
; 不是
不是 ,且
,且 , 证明:
, 证明: 为等边三角形.
为等边三角形.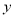 轴上的椭圆
轴上的椭圆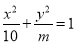 的长轴长为8,则
的长轴长为8,则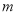 等于 ( )
等于 ( ) ,
, ,曲线
,曲线 及
及 轴所围成的封闭图形的面积是 ( )
轴所围成的封闭图形的面积是 ( ) B.
B. C.
C. D.
D.