题目内容
已知点P（x，y）满足（x+y-1）
=0，则点P运动后得到的图象为（ ）
| 4x2+9y2-36 |
| A、一直线和一椭圆 |
| B、一线段和一椭圆 |
| C、一射线和一椭圆 |
| D、两射线和一椭圆 |
考点：轨迹方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：点P（x，y）满足（x+y-1）
=0，可得x+y-1=0（4x2+9y2≥36）或4x2+9y2=36，即可得出结论．
| 4x2+9y2-36 |
解答：
解：∵点P（x，y）满足（x+y-1）
=0，
∴x+y-1=0（4x2+9y2≥36）或4x2+9y2=36，
∴点P运动后得到的图象为两射线和一椭圆．
故选：D．
| 4x2+9y2-36 |
∴x+y-1=0（4x2+9y2≥36）或4x2+9y2=36，
∴点P运动后得到的图象为两射线和一椭圆．
故选：D．
点评：本题考查轨迹方程，考查学生转化化归的能力，属于基础题．
练习册系列答案
相关题目
阅读下列程序：
如果输入x=-2，则输出结果y为（ ）
如果输入x=-2，则输出结果y为（ ）
| A、0 | B、-1 | C、-2 | D、9 |
已知命题p：lnx＞0，命题q：ex＞1，则命题p是命题q（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
若向量
=（1，2），
=（4，5），则
=（ ）
| BA |
| CA |
| BC |
| A、（5，7） |
| B、（-3，-3） |
| C、（3，3） |
| D、（-5，-7） |
设函数y=f（x）在区间（a，b）的导函数f′（x），f′（x）在区间（a，b）的导函数记为f″（x），若在区间（a，b）上的f″（x）＜0恒成立，则称函数f（x）在区间（a，b）上为“上凸函数”，已知f（x）=
x4-
mx3-
x2，若当实数m满足|m|≤2时，函数f（x）在区间（a，b）上为“上凸函数”，则区间（a，b）可以是（ ）
| 1 |
| 12 |
| 1 |
| 6 |
| 3 |
| 2 |
| A、（-1，3） |
| B、（0，1） |
| C、（-3，3） |
| D、（-3，1） |
若
=（x，3），
=（3，1）且
∥
，则x的值是（ ）
| a |
| b |
| a |
| b |
| A、-9 | B、-1 | C、1 | D、9 |
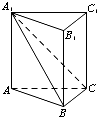如图，在直三棱柱ABC-A1B1C1中，平面A1BC⊥侧面A1ABB1．