题目内容
14．设等差数列{an}满足5a7=7a10，且a1＞0，Sn为其前n项和，则Sn中最大的是（ ）| A． | S16 | B． | S17 | C． | S18 | D． | S16或S17 |
分析 由题意表示出数列的公差，可得通项公式，可得等差数列{an}前17项为正数，从第18项起为负数，从而易得答案．
解答 解：设等差数列{an}的公差为d，
由5a7=7a10可得5（a1+6d）=7（a1+9d），
解得d=-$\frac{2}{33}$a1＜0，
∴an=a1+（n-1）d=$\frac{35-2n}{33}$a1，
令an=$\frac{35-2n}{33}$a1≤0可得$\frac{35-2n}{33}$≤0，
解得n≥$\frac{35}{2}$，
∴递减的等差数列{an}前17项为正数，从第18项起为负数，
∴数列{Sn}的最大项为S17，
故选：B．
点评 本题考查等差数列的前n项和的最值，从数列项的正负入手是解决问题的关键，属基础题．
练习册系列答案
相关题目
4．在△ABC中，A、B、C所对的边分别是a、b、c，$\overrightarrow{m}$=（b-a，a-c-b），$\overrightarrow{n}$=（a-c，b+c），若$\overrightarrow{m}$∥$\overrightarrow{n}$，且a（sinB-cosC）=c•cosA，则C等于（ ）
| A． | $\frac{π}{4}$ | B． | $\frac{π}{6}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
6．已知A（4，1，3），B（2，-5，1），C（3，7，-5），则平行四边形ABCD的顶点D的坐标是（ ）
| A． | （2，4，-1） | B． | （2，3，1） | C． | （-3，1，5） | D． | （5，13，-3） |
3．集合M={y|y=ex+$\frac{1}{2}$}，N={x∈N|0≤x+1≤3}，则M∩N等于（ ）
| A． | {1，2} | B． | {0，1，2} | C． | （$\frac{1}{2}$，2] | D． | {1，2，3} |
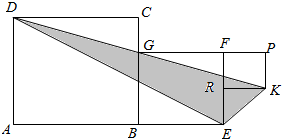正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示，点G在线段DK上，正方形BEFG的边长为4，则△DEK的面积为（ ）