题目内容
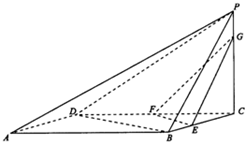 如图,四棱锥P-ABCD中,底面ABCD是平行四边形,PC⊥平面ABCD,PC=4,AB=6,BD=3
如图,四棱锥P-ABCD中,底面ABCD是平行四边形,PC⊥平面ABCD,PC=4,AB=6,BD=3| 3 |
(Ⅰ)求证:BD⊥平面PBC;
(Ⅱ)若E,F,G分别是线段BC,DC,PC上的动点,且EF=2,试探究多面体PDBGFE的体积是否存在最小值,若存在,求出最小值;若不存在,说明理由.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)证明DB⊥BC,PC⊥BD,即可证明BD⊥平面PBC;
(Ⅱ)当VG-ECF存在最大值时,多面体PDBGFE的体积最小.
(Ⅱ)当VG-ECF存在最大值时,多面体PDBGFE的体积最小.
解答:
(Ⅰ)证明:△BCD中,CD=AB=6,BD=3
,∠DCB=∠DAB=60°,
由正弦定理可得
=
,
∴sin∠CBD=1,
∴∠CBD=90°,
∴DB⊥BC,
∵PC⊥平面ABCD,BD?平面ABCD,
∴PC⊥BD,
∵BC∩PC=C,
∴BD⊥平面PBC;
(Ⅱ)解:VPDBGFE=VP-BCD-VG-ECF,
当VG-ECF存在最大值时,多面体PDBGFE的体积最小.
∵PC⊥平面ABCD,
∴VG-ECF=
S△ECF•GC.
当G运动到P时,PC=4.
设CE=a,CF=b,则
∵EF=2,
∴由余弦定理得a2+b2-ab=4,
∴4+ab=a2+b2≥2ab,
∴ab≤4(当且仅当a=b=2时等号成立).
∴S△ECF=
CE•CF•sin∠DCB=
ab≤
,
∴a=b=2时,(S△ECF)max=
,
∴(VG-ECF)max=
•
•4=
.
∵VP-BCD=
•
•4=6
,
∴多面体PDBGFE的体积的最小值为
.
| 3 |
由正弦定理可得
3
| ||
| sin60° |
| 6 |
| sin∠CBD |
∴sin∠CBD=1,
∴∠CBD=90°,
∴DB⊥BC,
∵PC⊥平面ABCD,BD?平面ABCD,
∴PC⊥BD,
∵BC∩PC=C,
∴BD⊥平面PBC;
(Ⅱ)解:VPDBGFE=VP-BCD-VG-ECF,
当VG-ECF存在最大值时,多面体PDBGFE的体积最小.
∵PC⊥平面ABCD,
∴VG-ECF=
| 1 |
| 3 |
当G运动到P时,PC=4.
设CE=a,CF=b,则
∵EF=2,
∴由余弦定理得a2+b2-ab=4,
∴4+ab=a2+b2≥2ab,
∴ab≤4(当且仅当a=b=2时等号成立).
∴S△ECF=
| 1 |
| 2 |
| ||
| 4 |
| 3 |
∴a=b=2时,(S△ECF)max=
| 3 |
∴(VG-ECF)max=
| 1 |
| 3 |
| 3 |
4
| ||
| 3 |
∵VP-BCD=
| 1 |
| 3 |
9
| ||
| 2 |
| 3 |
∴多面体PDBGFE的体积的最小值为
14
| ||
| 3 |
点评:本题考查线面垂直的证明,考查多面体体积是计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
随机变量Y满足P(Y=c)=1,其中c为常数,则D(Y)等于( )
| A、0 | B、c(1-c) | C、c | D、1 |
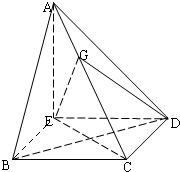 如图,在四棱锥A-BCDE中,AE⊥平面BCDE,∠ABC=∠BCD=∠CDA=90°,AC=6
如图,在四棱锥A-BCDE中,AE⊥平面BCDE,∠ABC=∠BCD=∠CDA=90°,AC=6