题目内容
如图,长方体 中,
中,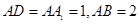 ,点E是AB的中点.
,点E是AB的中点.
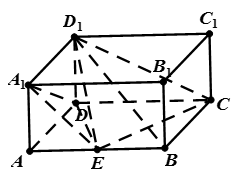
(1)求三棱锥 的体积;
的体积;
(2)证明: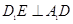 ;
;
(3)求二面角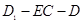 的正切值.
的正切值.
 中,
中,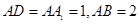 ,点E是AB的中点.
,点E是AB的中点.
(1)求三棱锥
 的体积;
的体积;(2)证明:
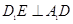 ;
; (3)求二面角
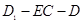 的正切值.
的正切值.(1)1;(2)详见解析;(3)

试题分析:(1)求四面体的体积,当高不好确定时候,可考虑等体积转化,该题中
 ,高
,高 ,可求体积;(2)证明直线和直线垂直,可先证明直线和平面垂直,由
,可求体积;(2)证明直线和直线垂直,可先证明直线和平面垂直,由 ,从而
,从而 面
面 ,所以
,所以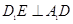 ,(3) 求二面角的平面角,可以利用几何法,先找到二面角的平面角,然后借助平面图形去计算,∵
,(3) 求二面角的平面角,可以利用几何法,先找到二面角的平面角,然后借助平面图形去计算,∵
 ,所以
,所以 ,进而可证
,进而可证 ,
, 就是
就是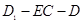 的平面角,二面角也可以利用空间向量法,建立适当的空间直角坐标系,把相关点的坐标表示出来,计算两个半平面的法向量,进而求法向量的夹角,然后得二面角的余弦值.
的平面角,二面角也可以利用空间向量法,建立适当的空间直角坐标系,把相关点的坐标表示出来,计算两个半平面的法向量,进而求法向量的夹角,然后得二面角的余弦值.试题解析:(1)解:在三棱锥D1-DCE中,D1D⊥平面DCE,D1D=1
在△DCE中,
 ,
,
CD=2,CD2=CE2+DE2 ∴CE⊥DE.
∴

∴三棱锥D1-DCE的体积
 . =
. = 4分
4分(2)证明:连结AD1,由题可知:四边形ADD1A1是正方形
∴A1D⊥AD1 又∵AE⊥平面ADD1A1,A1D
 平面ADD1A1
平面ADD1A1∴AB⊥AD1 又∵AB
 平面AD1E,AD1
平面AD1E,AD1 平面A D1E AB
平面A D1E AB AD1=A
AD1=A∴A1D⊥平面AD1E 又∵D1E
 平面AD1E
平面AD1E∴A1D⊥D1E 8分
(3)根据题意可得:D1D⊥平面ABCD
又因为CE
 平面ABCD,所以D1D⊥CE。
平面ABCD,所以D1D⊥CE。又由(1)中知,DE⊥CE,D1D
 平面D1DE,DE
平面D1DE,DE 平面D1DE,D1D
平面D1DE,D1D DE=D,
DE=D,∴CE⊥平面D1DE,又∵D1E
 平面D1DE ∴CE⊥D1E.
平面D1DE ∴CE⊥D1E.∴∠D1ED即为二面角D1―EC―D的一个平面角.
在Rt△D1DE中,∠D1DE=90°,D1D="1," DE=

∴

∴二面角D1―ED―D的正切值是
 12分
12分
练习册系列答案
相关题目
 和AB1的中点,点F在BC上且满足BF∶FC=1∶3.
和AB1的中点,点F在BC上且满足BF∶FC=1∶3.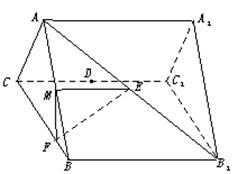
 的体积.
的体积. 中,底面
中,底面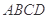 是正方形,侧面
是正方形,侧面 是正三角形,平面
是正三角形,平面 底面
底面
 为线段VC的中点,求证:
为线段VC的中点,求证: 平面
平面 ;
; 的体积
的体积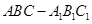 中,
中,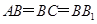 ,
,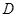 为
为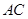 的中点.
的中点.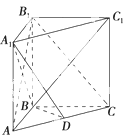
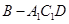 的体积.
的体积.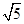 .
.
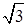 ,AD=CD=1.
,AD=CD=1.
 求证:BD⊥AA1;
求证:BD⊥AA1; 若四边形
若四边形 是菱形,且
是菱形,且 ,求四棱柱
,求四棱柱 的体积.
的体积. 和
和 ,较短腰长为
,较短腰长为



 ,那么正方体的棱长等于________。
,那么正方体的棱长等于________。



