题目内容
如图,椭圆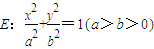 的右焦点F2与抛物线y2=4x的焦点重合,过F2作与x轴垂直的直线l与椭圆交于S,T,而与抛物线交于C,D两点,且
的右焦点F2与抛物线y2=4x的焦点重合,过F2作与x轴垂直的直线l与椭圆交于S,T,而与抛物线交于C,D两点,且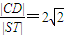 .
.(1)求椭圆E的方程;
(2)若过m(2,0)的直线与椭圆E相交于两点A和B,设P为椭圆E上一点,且满足
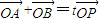 (O为坐标原点),求实数t的取值范围.
(O为坐标原点),求实数t的取值范围.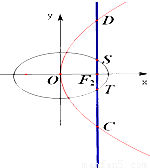
【答案】分析:(1)由焦点F2(1,0),过F2作与x轴垂直的直线l与椭圆交于S,T,而与抛物线交于C,D两点,且 ,知|CD|=4,|ST|=
,知|CD|=4,|ST|=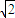 ,由此能求出椭圆方程.
,由此能求出椭圆方程.
(2)设过m(2,0)的直线为y=k(x-2),由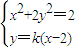 ,得(1+2k2)x2-8k2x+8k2-2=0,设A(x1,y1),B(x2,y2),P(x,y),
,得(1+2k2)x2-8k2x+8k2-2=0,设A(x1,y1),B(x2,y2),P(x,y),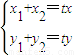 ,由此结合题设条件能求出实数t的取值范围.
,由此结合题设条件能求出实数t的取值范围.
解答:解:(1)∵椭圆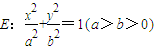 的右焦点F2与抛物线y2=4x的焦点重合,
的右焦点F2与抛物线y2=4x的焦点重合,
∴焦点F2(1,0),
∵过F2作与x轴垂直的直线l与椭圆交于S,T,而与抛物线交于C,D两点,且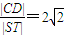 .
.
∴|CD|=4,解得|ST|=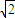 ,
,
∴a= ,b=1,c=1,
,b=1,c=1,
∴椭圆E的方程是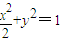 .
.
(2)设过m(2,0)的直线为y=k(x-2),
由 ,得(1+2k2)x2-8k2x+8k2-2=0,
,得(1+2k2)x2-8k2x+8k2-2=0,
设A(x1,y1),B(x2,y2),P(x,y), ,
,
则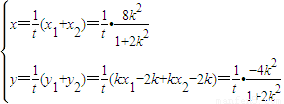 ,
,
2=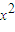 +2
+2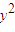 =
=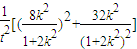 ,
,
∴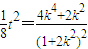 ,
,
∵△=(8k2)2-4(1+2k2)(8k2-2)>0,
∴0≤2k2<1,
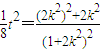 =1-
=1-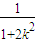 ,
,
∴t∈(-2,2).
点评:本题考查椭圆方程的求法,考查满足条件的实数的取值范围的求法,解题时要认真审题,注意等价转化思想的合理运用.
 ,知|CD|=4,|ST|=
,知|CD|=4,|ST|=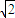 ,由此能求出椭圆方程.
,由此能求出椭圆方程.(2)设过m(2,0)的直线为y=k(x-2),由
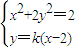 ,得(1+2k2)x2-8k2x+8k2-2=0,设A(x1,y1),B(x2,y2),P(x,y),
,得(1+2k2)x2-8k2x+8k2-2=0,设A(x1,y1),B(x2,y2),P(x,y),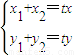 ,由此结合题设条件能求出实数t的取值范围.
,由此结合题设条件能求出实数t的取值范围.解答:解:(1)∵椭圆
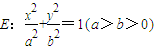 的右焦点F2与抛物线y2=4x的焦点重合,
的右焦点F2与抛物线y2=4x的焦点重合,∴焦点F2(1,0),
∵过F2作与x轴垂直的直线l与椭圆交于S,T,而与抛物线交于C,D两点,且
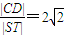 .
.∴|CD|=4,解得|ST|=
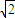 ,
,∴a=
 ,b=1,c=1,
,b=1,c=1,∴椭圆E的方程是
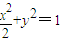 .
.(2)设过m(2,0)的直线为y=k(x-2),
由
 ,得(1+2k2)x2-8k2x+8k2-2=0,
,得(1+2k2)x2-8k2x+8k2-2=0,设A(x1,y1),B(x2,y2),P(x,y),
 ,
,则
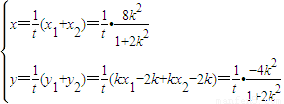 ,
,2=
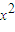 +2
+2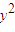 =
=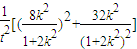 ,
,∴
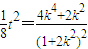 ,
,∵△=(8k2)2-4(1+2k2)(8k2-2)>0,
∴0≤2k2<1,
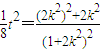 =1-
=1-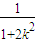 ,
,∴t∈(-2,2).
点评:本题考查椭圆方程的求法,考查满足条件的实数的取值范围的求法,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
相关题目
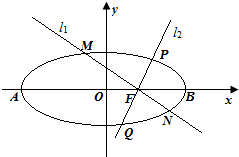 如图,椭圆的中心在坐标原点,长轴端点为A、B,右焦点为F,且
如图,椭圆的中心在坐标原点,长轴端点为A、B,右焦点为F,且 (2006•海淀区一模)如图,椭圆
(2006•海淀区一模)如图,椭圆
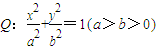 的右焦点为F(c,0),过点F的一动直线m绕点F转动,
的右焦点为F(c,0),过点F的一动直线m绕点F转动,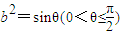 .
.
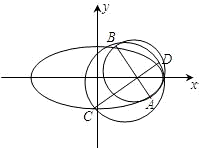 如图,椭圆
如图,椭圆 的右焦点为F,过焦点F作两条互相垂直的弦AB、CD,设弦AB、CD的中点分别为M、N.
的右焦点为F,过焦点F作两条互相垂直的弦AB、CD,设弦AB、CD的中点分别为M、N.