题目内容
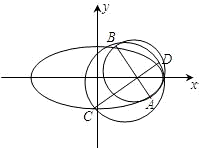 如图,椭圆
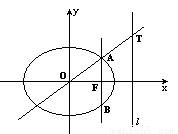
如图,椭圆 的右焦点为F,过焦点F作两条互相垂直的弦AB、CD,设弦AB、CD的中点分别为M、N.
的右焦点为F,过焦点F作两条互相垂直的弦AB、CD,设弦AB、CD的中点分别为M、N.
(Ⅰ)求证:直线MN恒过定点T,并求出T的坐标;
(Ⅱ)求以AB、CD为直径的两圆公共弦中点的轨迹方程,并判断定点T与轨迹的位置关系.
解:(Ⅰ)∵F(1,0),不妨设AB的斜率存在且不为零,
设AB:y=k(x-1)
∴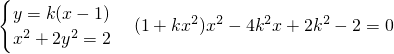
∴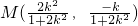 ,同理
,同理 (3分)
(3分)
∴MN过定点(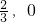 ),当AB的斜率不存在或为零时
),当AB的斜率不存在或为零时
同样MN过定点(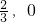 ),∴T(
),∴T(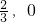 ). (7分)
). (7分)
(Ⅱ)以AB为直径的圆M的方程为:
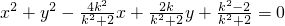 ①(9分)
①(9分)
同理以CD为直径的圆N的方程为:
 ②(11分)
②(11分)
①-②得公共弦直线方程为 ③
③
又MN直线方程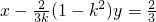 ④
④
由③、④消去R得两圆公共弦中点的轨迹方程为:(15分)

∴点T在圆上.
分析:(Ⅰ)设AB:y=k(x-1),由题意知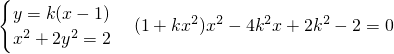 ,
,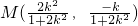 ,同理
,同理 ,所以MN过定点(
,所以MN过定点(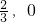 ),当AB的斜率不存在或为零时同样MN过定点(
),当AB的斜率不存在或为零时同样MN过定点(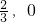 ),所以T(
),所以T(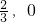 ).
).
(Ⅱ)以AB为直径的圆M的方程为: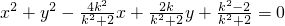 同理以CD为直径的圆N的方程为:
同理以CD为直径的圆N的方程为:
 ,由此可以判断定点T与轨迹的位置关系.
,由此可以判断定点T与轨迹的位置关系.
点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,仔细解题.
设AB:y=k(x-1)
∴
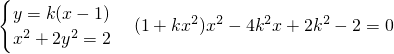
∴
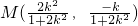 ,同理
,同理 (3分)
(3分)∴MN过定点(
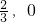 ),当AB的斜率不存在或为零时
),当AB的斜率不存在或为零时同样MN过定点(
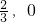 ),∴T(
),∴T(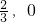 ). (7分)
). (7分)(Ⅱ)以AB为直径的圆M的方程为:
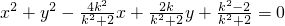 ①(9分)
①(9分)同理以CD为直径的圆N的方程为:
 ②(11分)
②(11分)①-②得公共弦直线方程为
 ③
③又MN直线方程
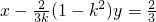 ④
④由③、④消去R得两圆公共弦中点的轨迹方程为:(15分)

∴点T在圆上.
分析:(Ⅰ)设AB:y=k(x-1),由题意知
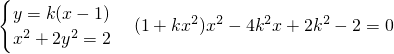 ,
,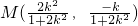 ,同理
,同理 ,所以MN过定点(
,所以MN过定点(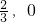 ),当AB的斜率不存在或为零时同样MN过定点(
),当AB的斜率不存在或为零时同样MN过定点(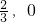 ),所以T(
),所以T(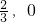 ).
).(Ⅱ)以AB为直径的圆M的方程为:
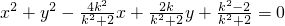 同理以CD为直径的圆N的方程为:
同理以CD为直径的圆N的方程为: ,由此可以判断定点T与轨迹的位置关系.
,由此可以判断定点T与轨迹的位置关系.点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,仔细解题.

练习册系列答案
相关题目

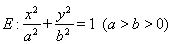
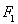
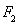
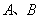
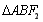
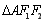
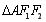

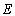
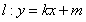
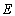
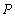
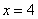
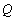
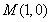
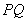
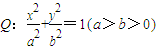 的右焦点为F(c,0),过点F的一动直线m绕点F转动,
的右焦点为F(c,0),过点F的一动直线m绕点F转动,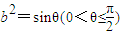 .
.
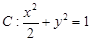 的右焦点为
的右焦点为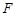 ,右准线为
,右准线为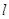 ,
,
 的轨迹方程。
的轨迹方程。 于点
于点 ,又直线
,又直线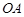 交
交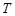 ,若
,若 ,
, 的长;
的长;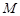 的坐标为
的坐标为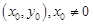 ,直线
,直线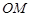 交直线
交直线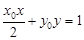 于点
于点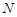 ,且和椭圆
,且和椭圆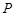 ,是否存在实数
,是否存在实数 ,使得
,使得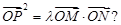 ,若存在,求出实数
,若存在,求出实数