题目内容
)
已知递增的等差数列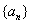 的首项
的首项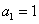 ,且
,且 、
、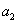 、
、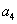 成等比数列.
成等比数列.
(1)求数列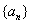 的通项公式
的通项公式 ;
;
(2)设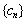 对任意
对任意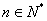 ,都有
,都有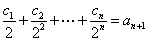 成立,求
成立,求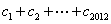 的值.
的值.
(3)若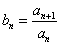
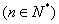 ,求证:数列
,求证:数列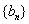 中的任意一项总可以表示成其他两项之积.
中的任意一项总可以表示成其他两项之积.
(1)∵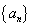 是递增的等差数列,设公差为
是递增的等差数列,设公差为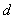
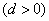
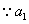 、
、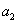 、
、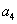 成等比数列
成等比数列
∴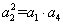 由
由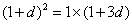 及
及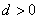 得
得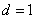 ∴
∴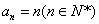
(2)∵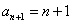 ,
,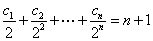 对
对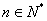 都成立
都成立
当 时,
时, 得
得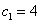
当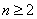 时,由
时,由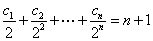 ①,及
①,及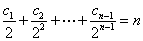 ②
②
①-②得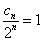 ,得
,得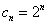 ∴
∴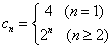
∴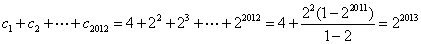
(3)对于给定的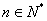 ,若存在
,若存在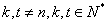 ,使得
,使得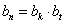
∵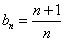 ,只需
,只需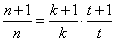 ,即
,即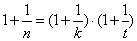 ,即
,即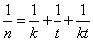
即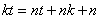 ,
,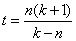 取
取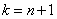 ,则
,则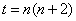
∴对数列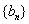 中的任意一项
中的任意一项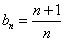
 ,都存在
,都存在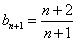 和
和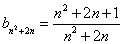
使得

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 是定义在非零实数集上的函数,
是定义在非零实数集上的函数, 时,
时, ,记
,记 ,则 ( )
,则 ( ) B.
B. C.
C. D.
D.
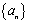 的前
的前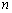 项和为
项和为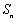 ,满足
,满足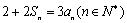 .数列
.数列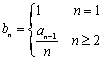 .
.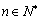 ,不等式
,不等式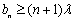 恒成立,求实数
恒成立,求实数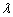 的最大值.
的最大值.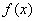 是定义在R上的偶函数,对任意
是定义在R上的偶函数,对任意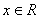 ,都有
,都有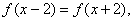 且当
且当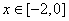 时,
时, .若在区间
.若在区间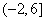 内关于
内关于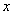 的方程
的方程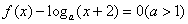 恰有3个不同的实数根,则实数
恰有3个不同的实数根,则实数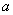 的取值范围是( )
的取值范围是( ) B.
B.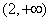 C.
C.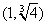 D.
D.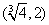
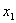 ,
,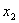 ,
,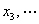 ,
, 的方差为
的方差为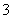 ,则
,则 ,
,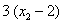 ,
,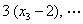 ,
,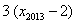 的方差为
的方差为 ( )
( )
 C.
C. 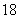 D.
D. 
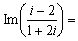 .
.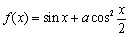 (
(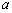 为常数,
为常数,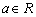 ),且
),且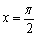 是方程
是方程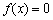 的解.当
的解.当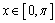
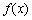 值域为 .
值域为 .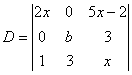 ,元素
,元素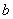
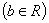 的代数余子式为
的代数余子式为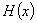 ,
,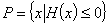 , 函数
, 函数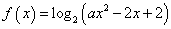 的定义域为
的定义域为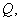 若
若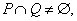 求实数
求实数 的取值范围.
的取值范围. (
( )的最大值等于 .
)的最大值等于 .