题目内容
在公差不为0的等差数列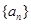 中,
中,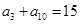 ,且
,且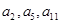 成等比数列.
成等比数列.
(1)求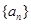 的通项公式;
的通项公式;
(2)设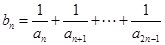 ,证明:
,证明: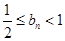 .
.
(1)an=n+1;(2)证明过程详见解析.
解析试题分析:本题主要考查等差数列的通项公式、等比中项、放缩法、数列的单调性等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,先用等比中项的定义将数学语言转化为数学表达式,再用等差数列的通项公式将已知的所有表达式都用 和
和 展开,解方程组解出基本量
展开,解方程组解出基本量 和
和 ,利用等差数列的通项公式写出数列
,利用等差数列的通项公式写出数列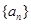 的通项公式;第二问,先利用单调性的定义,利用
的通项公式;第二问,先利用单调性的定义,利用 来判断数列
来判断数列 单调递增,所以最小值为
单调递增,所以最小值为 ,从而证明
,从而证明 ,再利用放缩法证明
,再利用放缩法证明 .
.
试题解析:(1)设等差数列{an}的公差为d.由已知得 ,
,
注意到d≠0,解得a1=2,d=1.
所以an=n+1. 4分
(2)由(1)可知 ,
, ,
,
因为 ,
,
所以数列{bn}单调递增. 8分 . 9分
. 9分
又 ,
,
因此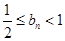 . 12分
. 12分
考点:等差数列的通项公式、等比中项、放缩法、数列的单调性.

练习册系列答案
相关题目
 (n∈N*).
(n∈N*). ,计算a2,a3,a4的值,并求出数列{an}的通项公式.
,计算a2,a3,a4的值,并求出数列{an}的通项公式. 满足
满足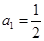 ,
, .
. 的值,由此猜测
的值,由此猜测 .
. 的首项
的首项 ,公差
,公差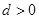 ,且第
,且第 项、第
项、第 项、第
项、第 项分别是等比数列
项分别是等比数列 项、第
项、第 项.
项. 对任意
对任意 ,均有
,均有 成立.
成立. ; ②求
; ②求 .
.
 ,若该集合具有下列性质的子集:每个子集至少含有2个元素,且每个子集中任意两个元素之差的绝对值大于1,则称这些子集为
,若该集合具有下列性质的子集:每个子集至少含有2个元素,且每个子集中任意两个元素之差的绝对值大于1,则称这些子集为 子集,记
子集,记 .
. 时,写出所有
时,写出所有 ;
; ,求证:
,求证:
 为等差数列,
为等差数列, ,其前n项和为
,其前n项和为 ,若
,若 ,
, 值.
值.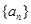 的前
的前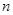 项和为
项和为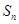 ,
,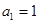 ,且
,且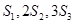 成等差数列.
成等差数列. ,求数列
,求数列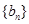 的前
的前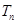 .
. 前n项和
前n项和 =
= (
(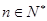 ), 数列
), 数列 为等比数列,首项
为等比数列,首项 =2,公比为q(q>0)且满足
=2,公比为q(q>0)且满足 ,
, ,
, 为等比数列.
为等比数列. ,记数列
,记数列 为等差数列,且
为等差数列,且 .
. 项和
项和 ;
; 满足
满足 求数列
求数列