题目内容
11.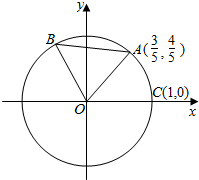 已知A、B是单位圆O上的点,且点B在第二象限,点C是圆O与x轴正半轴的交点,点A的坐标为$(\frac{3}{5},\frac{4}{5})$,若△AOB为正三角形.
已知A、B是单位圆O上的点,且点B在第二象限,点C是圆O与x轴正半轴的交点,点A的坐标为$(\frac{3}{5},\frac{4}{5})$,若△AOB为正三角形.(Ⅰ)若设∠COA=θ,求sin2θ的值;
(Ⅱ)求cos∠COB的值.
分析 (Ⅰ)根据A的坐标,利用三角函数的定义可知cosθ=$\frac{3}{5}$,sinθ=$\frac{4}{5}$,利用二倍角公式求sin2θ的值;
(Ⅱ)利用角的变换,化简cos∠COB=cos(∠COA+60°)展开,即可求cos∠COB.
解答 解:(1)因为A点的坐标为$(\frac{3}{5},\frac{4}{5})$,根据三角函数定义可知cosθ=$\frac{3}{5}$,sinθ=$\frac{4}{5}$,…(3)分
∴sin2θ=2sinθcosθ=$\frac{24}{25}$.…(6)分
(2)因为三角形AOB为正三角形,所以∠AOB=60°,
cos∠COA=$\frac{3}{5}$,sin∠COA=$\frac{4}{5}$,
所以cos∠COB=cos(∠COA+60°)=cos∠COAcos60°-sin∠COAsin60°=$\frac{3-4\sqrt{3}}{10}$.…(12)分
点评 本题是基础题,考查三角函数的定义,解答变换的技巧,两角和的余弦函数的应用,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.设命题p:若2x>3x,则x<0,其逆否命题为( )
| A. | 若x≥0,则2x≤3x | B. | 若x>0,则 2x<3x | C. | 若2x>3x,则x≥0 | D. | 若2x≤3x,则x>0 |
16.函数f(x)=5|x|的值域是( )
| A. | (-∞,1] | B. | [1,+∞) | C. | (0,1] | D. | (0,+∞) |




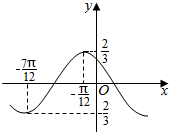 函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)图象的一段如图所示
函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)图象的一段如图所示