题目内容
(08年福州质检理)(12分)
已知![]() 上不相同的两个点,l是弦AB的垂直平分线.
上不相同的两个点,l是弦AB的垂直平分线.
(1)当![]() +
+![]() 取何值时,可使抛物线的焦点F与原点O到直线l的距离相等?证明你的结论;
取何值时,可使抛物线的焦点F与原点O到直线l的距离相等?证明你的结论;
(2)当直线l的斜充为1时,求l在y轴上截距的取值范围.
解析:(1)由已知,抛物线![]() ,焦点F的坐标为F(0,1)………………1分
,焦点F的坐标为F(0,1)………………1分
当l与y轴重合时,显然符合条件,此时![]() ……………………3分
……………………3分
当l不与y轴重合时,要使抛物线的焦点F与原点O到直线l的距离相等,当且仅当直线l通过点(![]() )设l的斜率为k,则直线l的方程为
)设l的斜率为k,则直线l的方程为![]()
由已知可得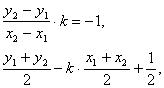 即
即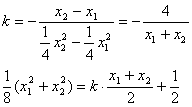 ………5分
………5分
解得![]() 无意义.
无意义.
因此,只有![]() 时,抛物线的焦点F与原点O到直线l的距离相等.……7分
时,抛物线的焦点F与原点O到直线l的距离相等.……7分
(2)由已知可设直线l的方程为![]() ……………………8分
……………………8分
则AB所在直线为![]() ……………………9分
……………………9分
代入抛物线方程![]() ………………①
………………①
∴![]() 的中点为
的中点为![]()
代入直线l的方程得:![]() ………………10分
………………10分
又∵对于①式有:![]()
解得m>-1,
∴![]()
∴l在y轴上截距的取值范围为(3,+![]() )……………………12分
)……………………12分

练习册系列答案
相关题目