Question

（08年福州质检理）（12分）

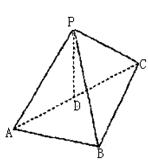
如图，P―ABC中，D是AC的中点，PA=PB=PC=

   （1）求证：PD⊥平面ABC；

   （2）求二面角P―AB―C的大小；

   （3）求AB的中点E到平面PBC的距离.

 

Answer 1

解析：方法一：

（1）证明：连结BD，

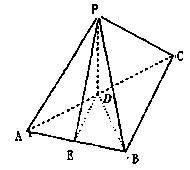
∵D分别是AC的中点，PA=PC=

∴PD⊥AC，

∵AC=2，AB=，BC=

∴AB²+BC²=AC²，

∴∠ABC=90°，即AB⊥BC.…………2分

∴BD=，

∵PD²=PA²―AD²=3，PB

∴PD²+BD²=PB²，

∴PD⊥BD，

∵ACBD=D

∴PD⊥平面ABC.…………………………4分

（2）解：取AB的中点E，连结DE、PE，由E为AB的中点知DE//BC，

∵AB⊥BC，

∴AB⊥DE，

∵DE是直线PE的底面ABC上的射景

∴PE⊥AB

∴∠PED是二面角P―AB―C的平面角，……………………6分

在△PED中，DE=∠=90°，

∴tan∠PDE=

∴二面角P―AB―C的大小是

（3）解：设点E到平面PBC的距离为h.

∵V_P―EBC=V_E―PBC，

∴……………………10分

在△PBC中，PB=PC=，BC=

而PD=

∴

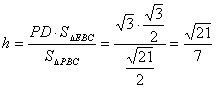
∴点E到平面PBC的距离为……………………12分

方法二：

（1）同方法一：

（2）解：解：取AB的中点E，连结DE、PE，

过点D作AB的平行线交BC于点F，以D为

原点，DE为x轴，DF为y轴，

DP为z轴，建立如图所示的空间直角坐标系.

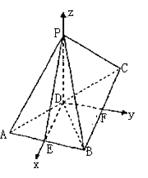
则D（0，0，0），P（0，0，），

E（），B=（）

设上平面PAB的一个法向量，

则由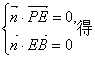

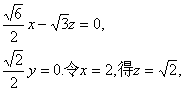
这时，……………………6分

显然，是平面ABC的一个法向量.

∴

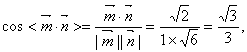
∴二面角P―AB―C的大小是……………………8分

（3）解：

设平面PBC的一个法向量，

由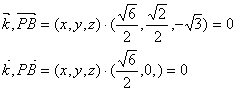

得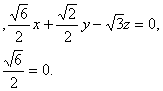

令是平面PBC的一个法向量……………………10分

又

∴点E到平面PBC的距离为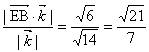………………12分