题目内容
等比数列 的前
的前 项和为
项和为 ,公比
,公比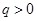 ,已知
,已知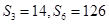 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若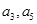 分别为等差数列
分别为等差数列 的第4项和第16项,试求数列
的第4项和第16项,试求数列 的通项公式及前
的通项公式及前 项和
项和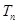 .
.
(1) ;(2)
;(2) ,
, .
.
解析试题分析:(1)等比数列基本量的求解是等比数列的一类基本问题,解决这类问题的关键在于熟练掌握等比数列的有关公式并能灵活运用,尤其需要注意的是,在使用等比数列的前 项和公式时,应该要分类讨论,有时还应善于运用整体代换的思想简化运算过程;(2)等差数列基本量的求解是等差数列的一类基本问题,解决这类问题的关键在于熟练掌握等差数列的有关公式并能灵活运用;(3)解题时要善于类比要能正确区分等差、等比的性质,不要把两者的性质搞混了.
项和公式时,应该要分类讨论,有时还应善于运用整体代换的思想简化运算过程;(2)等差数列基本量的求解是等差数列的一类基本问题,解决这类问题的关键在于熟练掌握等差数列的有关公式并能灵活运用;(3)解题时要善于类比要能正确区分等差、等比的性质,不要把两者的性质搞混了.
试题解析:解:(1)易知 ,由已知得
,由已知得 ,解得
,解得 .所以
.所以 . 4分
. 4分
(2)由(1)得 ,
, ,则
,则 ,
, ,
,
设 的公差为
的公差为 ,则有
,则有 解得
解得 6分
6分
且数列 的前
的前 项和
项和
 8分
8分
考点:(1)等比数列的通项公式;(2)等差数列的通行公式及前 项和公式.
项和公式.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
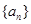 中,
中,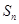 是它的前
是它的前 项之和,且
项之和,且 ,则
,则 ②
② 一定小于
一定小于 ③
③ 是各项中最大的项 ④
是各项中最大的项 ④ 一定是
一定是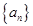 的前n项和为
的前n项和为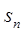 ,若
,若

 },
}, =25,
=25,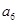 =15,数列{
=15,数列{ }的前n项和为
}的前n项和为
 }的前
}的前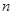 项和
项和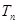 .
.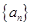 是等差数列,
是等差数列,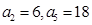 ,数列
,数列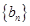 的前
的前 项和为
项和为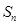 ,且
,且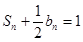 .
.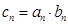 ,若
,若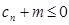 对任意的
对任意的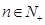 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.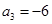 ,
,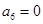 .
.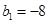 ,
, ,求
,求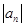 ,
, 。
。 的等差数列,已知它的前10项和为
的等差数列,已知它的前10项和为 ,且a1,a2,a4 成等比数列.
,且a1,a2,a4 成等比数列.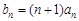 ,求数列
,求数列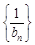 的前
的前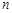 项和Tn .
项和Tn .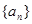 为等差数列,若
为等差数列,若 ,且它的前
,且它的前 项和
项和 有最小值,那么当
有最小值,那么当