题目内容
递减的等差数列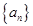 的前n项和为
的前n项和为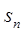 ,若
,若
(1)求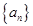 的等差通项;
的等差通项;
(2)当n为多少时,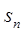 取最大值,并求出其最大值;
取最大值,并求出其最大值;
(3)求
(1)  ="12-n" ;(2) ,当n="11" 或 n=12时,
="12-n" ;(2) ,当n="11" 或 n=12时, 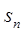 最大=66;
最大=66;
(3) =
=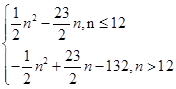 .
.
解析试题分析:(1)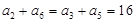 ,
,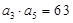



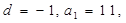

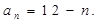
(2) 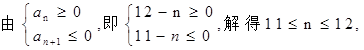
所以当n=11或n=12时,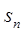 取最大值为66;
取最大值为66;
(3)由(2)知,当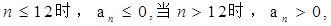
当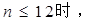

=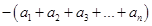
=-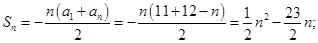
当n>12时, =
=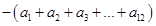
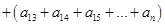
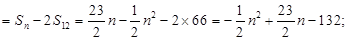
所以 =
=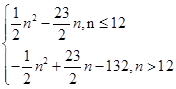 .
.
试题解析:(1) 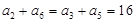 ,又
,又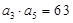 .
.
所以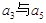 是方程
是方程 的两根,
的两根,
解得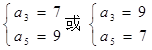 ,
,
又该等差数列递减,所以 ,
,
则公差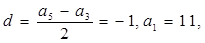
所以
(2)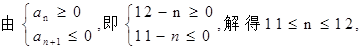
又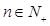 ,所以当n=11或n=12时,
,所以当n=11或n=12时,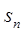 取最大值,
取最大值,
为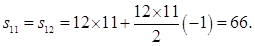
(3)由(2)知,当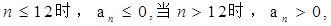
当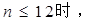
 =
=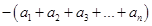
=-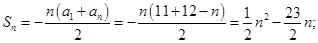
当n>12时, =
=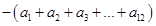
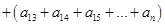
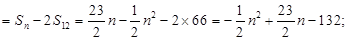
所以 =
=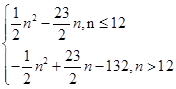 .
.
考点:数列综合题.等差数列的通项公式,等差数列的前n项和.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
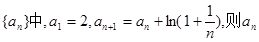 =
=  所有项均为正数,首
所有项均为正数,首 ,且
,且 成等差数列.
成等差数列. 的前n项和为
的前n项和为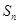 ,若
,若 ,求实数
,求实数 的值.
的值. 的前
的前 项和为
项和为 ,公比
,公比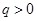 ,已知
,已知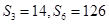 .
.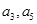 分别为等差数列
分别为等差数列 的第4项和第16项,试求数列
的第4项和第16项,试求数列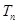 .
. 的前
的前 项和
项和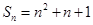 ,
,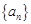 中,
中,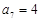 ,
,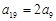 .
.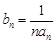 ,求数列
,求数列 的前
的前 项和
项和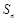 .
.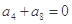 ,则使前n项和Sn取最值的正整数n="__________" .
,则使前n项和Sn取最值的正整数n="__________" .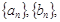
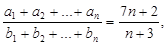 则
则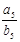 =___________.
=___________.