题目内容
已知数列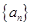 是等差数列,
是等差数列,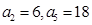 ,数列
,数列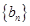 的前
的前 项和为
项和为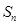 ,且
,且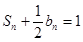 .
.
(1)求数列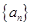 的通项公式;
的通项公式;
(2)记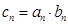 ,若
,若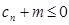 对任意的
对任意的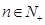 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1)
(2)
解析试题分析:(1)根据等差数列的首项和公差求通项公式;(2)由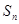 推
推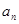 时,别漏掉
时,别漏掉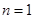 这种情况,大部分学生好遗忘;利用作差法判断数列的单调性;对于恒成立的问题,常用到以下两个结论:
这种情况,大部分学生好遗忘;利用作差法判断数列的单调性;对于恒成立的问题,常用到以下两个结论:
(1)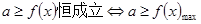 ,(2)
,(2)
试题解析:解答:(Ⅰ)由已知得 ,解得
,解得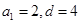 所以
所以 4分
4分
(Ⅱ)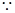
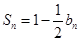 ,(1)
,(1)
当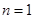 时,
时,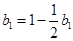 ,
, 当
当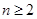 时,
时, (2)
(2)
(1)-(2)得 所以
所以 是以
是以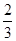 为首项,
为首项, 为公比的等比数列
为公比的等比数列
(Ⅲ)由(Ⅱ)知,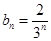 ,所以
,所以
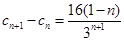 --
-- 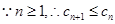
所以当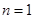 时,
时,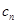 取到最大值
取到最大值 ,所以
,所以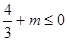 ,即
,即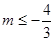 12分
12分
考点:(1)等差数列的通项公式,(2)等比数列的判断;(3)判断数列的单调性.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
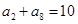 ,前
,前 项和为
项和为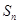 ,则
,则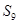 = .
= . 所有项均为正数,首
所有项均为正数,首 ,且
,且 成等差数列.
成等差数列. 的前n项和为
的前n项和为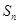 ,若
,若 ,求实数
,求实数 的值.
的值. 的前
的前 项和为
项和为 ,公比
,公比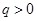 ,已知
,已知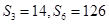 .
.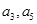 分别为等差数列
分别为等差数列 的第4项和第16项,试求数列
的第4项和第16项,试求数列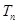 .
.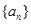 满足:
满足: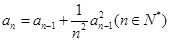
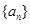 是以常数
是以常数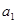 为首项,公差也为
为首项,公差也为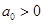 ,求证:
,求证: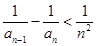 对任意
对任意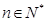 都成立;
都成立;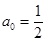 ,求证:
,求证: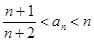 对任意
对任意 的前
的前 项和
项和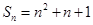 ,
,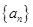 的通项公式为
的通项公式为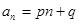 ,其中
,其中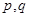 是常数,且
是常数,且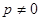 .
.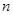 项和为
项和为 ,且
,且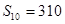 ,
,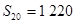 ,试确定
,试确定 的公式.
的公式.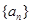 的公差为
的公差为 ,点
,点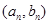 在函数
在函数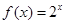 的图象上(
的图象上( ).
).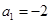 ,点
,点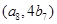 在函数
在函数 的图象上,求数列
的图象上,求数列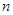 项和
项和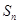 ;
;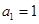 ,学科网函数
,学科网函数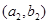 处的切线在
处的切线在 轴上的截距为
轴上的截距为 ,求数列
,求数列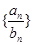 的前
的前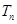 .
.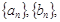
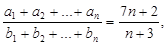 则
则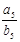 =___________.
=___________.