题目内容
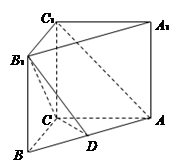
直三棱柱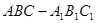 中,
中,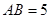 ,
,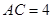 ,
,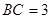 ,
,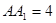 ,点D在
,点D在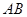 上.
上.
(1)求证: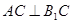 ;
;
(2)若D是AB中点,求证:AC1∥平面B1CD;
(3)当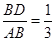 时,求二面角
时,求二面角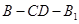 的余弦值.
的余弦值.
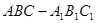 中,
中,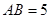 ,
,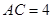 ,
,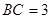 ,
,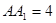 ,点D在
,点D在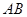 上.
上. 
(1)求证:
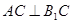 ;
;(2)若D是AB中点,求证:AC1∥平面B1CD;
(3)当
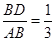 时,求二面角
时,求二面角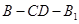 的余弦值.
的余弦值.(Ⅰ)证明略(Ⅱ)证明略 (Ⅲ)二面角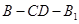 的余弦值为
的余弦值为 .
.
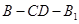 的余弦值为
的余弦值为 .
.本试题主要是考查了立体几何中的线面平行的证明,以及线线垂直的证明和二面角的求解的综合运用。
(1)根据已知条件我们知道,AC⊥BC.再结合三棱柱的性质可知线面垂直,然后利用线线垂直得到证明。
(2)要证明线面平行,一般先证明线线平行,然后结合判定定理得到结论。
(3)合理的建立空间直角坐标系,然后利用平面的法向量,借助于向量的夹角公式得到二面角的平面角的表示。
(1)根据已知条件我们知道,AC⊥BC.再结合三棱柱的性质可知线面垂直,然后利用线线垂直得到证明。
(2)要证明线面平行,一般先证明线线平行,然后结合判定定理得到结论。
(3)合理的建立空间直角坐标系,然后利用平面的法向量,借助于向量的夹角公式得到二面角的平面角的表示。

练习册系列答案
相关题目
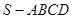 中,底面
中,底面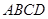 是直角梯形,
是直角梯形,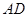 ∥
∥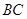 ,
,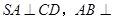 平面
平面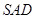 ,点
,点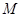 是
是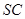 的中点,且
的中点,且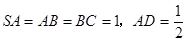 .
.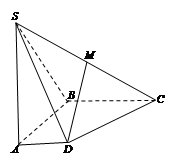
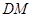 ∥平面
∥平面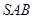 ;
; 的面积为8,当矩形周长取最小值时,沿对角线
的面积为8,当矩形周长取最小值时,沿对角线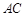 把
把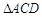 折起,则三棱锥
折起,则三棱锥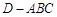 的外接球的表面积为________
的外接球的表面积为________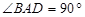 ,
,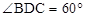 ,BC⊥CD .
,BC⊥CD .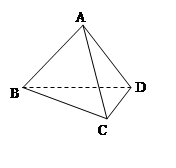
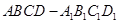 中,
中,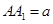 ,
,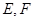 分别是
分别是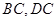 的中点,则异面直线
的中点,则异面直线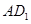 与
与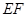 所成角为
所成角为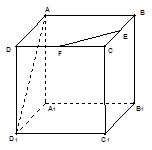
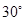
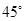
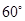
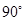
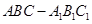 中,侧棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点。
中,侧棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点。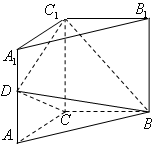
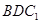 ⊥平面
⊥平面