Question

已知椭圆C的长轴长为，一个焦点的坐标为(1,0)．

（Ⅰ）求椭圆C的标准方程；

（Ⅱ）设直线l：y=kx与椭圆C交于A，B两点，点P为椭圆的右顶点．

（ⅰ）若直线l斜率k=1，求△ABP的面积；

（ⅱ）若直线AP，BP的斜率分别为，，求证：为定值．

（实际上，P是不同于A，B的任一点，结论都成立．）

Answer 1

解：（Ⅰ）依题意椭圆的焦点在x轴上，且，，

∴，    ．

∴椭圆C的标准方程为．              

（Ⅱ）（ⅰ）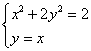               

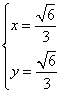∴    或 ，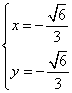              

即，， ．

所以．                            

（ⅱ）证明：设，．

椭圆的右顶点为

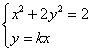  ， 消y整理得 ，

不妨设x₁>0>x₂，

∴ ，；，．

   ………

      

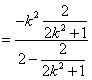
∴ 为定值．