题目内容
已知椭圆C:| x2 |
| 16 |
| y2 |
| 9 |
分析:设弦中点为M(x,y),交点为A(x1,y1),B(x2,y2).当M与P不重合时,A、B、M、P四点共线.故(y2-y1)(x-1)=(x2-x1)(y-2).再由点差法知
=-
,由此可得:9x2+16y2-9x-32y=0.
| 2x(x1-x2) |
| 16 |
| 2y(y1-y2) |
| 9 |
解答:解:设弦中点为M(x,y),交点为A(x1,y1),B(x2,y2).当M与P不重合时,A、B、M、P四点共线.
∴(y2-y1)(x-1)=(x2-x1)(y-2),①
由
+
=1,
+
=1两式相减得
+
=0.
又x1+x2=2x,y1+y2=2y,
∴
=-
,②
由①②可得:9x2+16y2-9x-32y=0,③
当点M与点P重合时,点M坐标为(1,2)适合方程③,
∴弦中点的轨迹方程为:9x2+16y2-9x-32y=0.
∴(y2-y1)(x-1)=(x2-x1)(y-2),①
由
| x12 |
| 16 |
| y12 |
| 9 |
| x22 |
| 16 |
| y22 |
| 9 |
| (x1-x2) (x1+x2) |
| 16 |
| (y1-y2) (y1+y2) |
| 9 |
又x1+x2=2x,y1+y2=2y,
∴
| 2x(x1-x2) |
| 16 |
| 2y(y1-y2) |
| 9 |
由①②可得:9x2+16y2-9x-32y=0,③
当点M与点P重合时,点M坐标为(1,2)适合方程③,
∴弦中点的轨迹方程为:9x2+16y2-9x-32y=0.
点评:本题考查轨迹方程的求法,解题时要注意点差法的合理运用.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
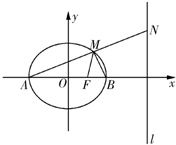 如图,已知椭圆
如图,已知椭圆