题目内容

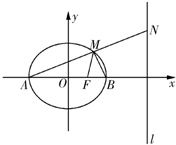精英家教网如图，已知椭圆C：
x2
16
+
y2
12
=1的左、右顶点分别为A、B，右焦点为F，直线l为椭圆的右准线，N为l上一动点，且在x轴上方，直线AN与椭圆交于点M．
（1）若AM=MN，求∠AMB的余弦值；
（2）设过A，F，N三点的圆与y轴交于P，Q两点，当线段PQ的中点坐标为（0，9）时，求这个圆的方程．
分析：（1）根据统一可知直线l的方程，设N（8，t）（t＞0），因为AM=MN，所以M（2，
t
2
），由M在椭圆上，得t=6．可求出点M的坐标，求出向量
MA
，
MB
，然后利用向量的夹角公式进行求解即可；
（2）设圆的方程为x2+y2+Dx+Ey+F=0，将A，F，N三点坐标代入，即可求出圆的方程，令x=0，得y2-(t+
72
t
)y-8=0，最后根据线段PQ的中点坐标为（0，9），t+
72
t
=18求出t，从而求出圆的方程．
解答：解：（1）由已知，A（-4，0），B（4，0），F（2，0），直线l的方程为x=8．
设N（8，t）（t＞0），因为AM=MN，所以M（2，
t
2
）．
由M在椭圆上，得t=6．故所求的点M的坐标为M（2，3）．（4分）
所以
MA
=(-6，-3)，
MB
=(2，-3)，
MA
•
MB
=-12+9=-3．cos∠AMB=
MA
•
MB
|
MA
||
MB
|
=
-3
36+9
•
4+9
=-
65
65
．（7分）
（2）设圆的方程为x2+y2+Dx+Ey+F=0，将A，F，N三点坐标代入，
得
16-4D+F=0
4+2D+F=0
64+t2+8D+Et+F=0
?
D=2
E=-t-
72
t
F=-8.

∵圆方程为x2+y2+2x-(t+
72
t
)y-8=0，令x=0，得y2-(t+
72
t
)y-8=0．（11分）
设P（0，y1），Q（0，y2），则y1、2=
t+
72
t
±
(t+
72
t
)2+32
2
．
由线段PQ的中点坐标为（0，9），得y1+y2=18，t+
72
t
=18．
此时所求圆的方程为x2+y2+2x-18y-8=0．（15分）
点评：本题主要考查了椭圆的性质以及利用向量法求夹角，同时考查了圆的方程，分析问题解决问题的能力，属于中档题．
练习册系列答案
相关题目
精英家教网如图，已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的焦点和上顶点分别为F1、F2、B，我们称△F1BF2为椭圆C的特征三角形．如果两个椭圆的特征三角形是相似的，则称这两个椭圆是“相似椭圆”，且三角形的相似比即为椭圆的相似比．
（1）已知椭圆C1：
x2
4
+y2=1和C2：
x2
16
+
y2
4
=1，判断C2与C1是否相似，如果相似则求出C2与C1的相似比，若不相似请说明理由；
（2）已知直线l：y=x+1，在椭圆Cb上是否存在两点M、N关于直线l对称，若存在，则求出函数f（b）=|MN|的解析式．
如图，已知椭圆C：
x2
a2
+
y2
b2
=1的离心率为
3
2
，过椭圆C上一点P（2，1）作倾斜角互补的两条直线，分别与椭圆交于点A、B，直线AB与x轴交于点M，与y轴负半轴交于点N．
（Ⅰ）求椭圆C的方程：
（Ⅱ）若S△PMN=
3
2
，求直线AB的方程．
如图，已知椭圆C：
x2
36
+
y2
20
=1的左顶点，右焦点分别为A，F，右准线为l，N为l上一点，且在x轴上方，AN与椭圆交于点M．
（1）若AM=MN，求证：AM⊥MF；
（2）过A，F，N三点的圆与y轴交于P，Q两点，求PQ的最小值．
（2012•深圳一模）如图，已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的离心率为
3
2
，以椭圆C的左顶点T为圆心作圆T：（x+2）2+y2=r2（r＞0），设圆T与椭圆C交于点M与点N．
（1）求椭圆C的方程；
（2）求
TM
•
TN
的最小值，并求此时圆T的方程；
（3）设点P是椭圆C上异于M，N的任意一点，且直线MP，NP分别与x轴交于点R，S，O为坐标原点，求证：|OR|•|OS|为定值．
精英家教网如图，已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左顶点，右焦点分别为A、F，右准线为m．圆D：x2+y2+x-3y-2=0．
（1）若圆D过A、F两点，求椭圆C的方程；
（2）若直线m上不存在点Q，使△AFQ为等腰三角形，求椭圆离心率的取值范围．
（3）在（1）的条件下，若直线m与x轴的交点为K，将直线l绕K顺时针旋转
π
4
得直线l，动点P在直线l上，过P作圆D的两条切线，切点分别为M、N，求弦长MN的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网