题目内容
19.已知直线l1经过点(0,1),直线l2过点(5,0),且l1∥l2.(1)若l1与l2距离为5,求两直线的方程;
(2)若l1与l2之间的距离最大,求最大距离,并求此时两直线的方程.
分析 (1)分类讨论:若l1、l2的斜率不存在,通过验证即可得出;若l1,l2的斜率都存在时,利用两条平行线的斜率之间的关系得出两条直线的方程,进而得到平行线之间的距离.
(2)当经过两点的直线与两点连线垂直时,距离最大.
解答 解:(1)①若l1,l2的斜率都存在时,
设直线的斜率为k,由斜截式得l1的方程y=kx+1,即kx-y+1=0.
由点斜式可得l2的方程y=k(x-5),即kx-y-5k=0.
在直线l1上取点A(0,1),
则点A到直线l2的距离d=$\frac{|1+5k|}{\sqrt{1+{k}^{2}}}$=5,
∴25k2+10k+1=25k2+25,
∴k=$\frac{12}{5}$.
∴l1:12x-5y+5=0,l2:12x-5y-60=0.
②若l1、l2的斜率不存在,
则l1的方程为x=0,l2的方程为x=5,它们之间的距离为5.同样满足条件.
(2)当经过两点的直线与两点连线垂直时,距离最大,此时斜率k=5,最大距离为$\sqrt{26}$,
l1:5x-y+1=0,l2:5x-y-25=0.
点评 本题考查了平行线之间的斜率关系及其距离、分类讨论等基础知识与基本技能方法,属于中档题.

练习册系列答案
相关题目
14.若△ABC的面积S△ABC∈[$\frac{\sqrt{3}}{2}$,$\frac{3\sqrt{3}}{2}$],且$\overrightarrow{AB}$•$\overrightarrow{BC}$=3,则向量$\overrightarrow{BA}$与$\overrightarrow{BC}$夹角的取值范围是( )
| A. | [$\frac{π}{3}$,$\frac{π}{2}$] | B. | [$\frac{3π}{4}$,$\frac{5π}{6}$] | C. | [$\frac{2π}{3}$,π) | D. | [$\frac{2π}{3}$,$\frac{5π}{6}$] |
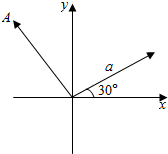 如图,点A的坐标为(-2,3),向量$\overrightarrow{a}$的模为4,则向量$\overrightarrow{OA}$的坐标为(-2,3),向量$\overrightarrow{a}$的坐标为(2$\sqrt{3}$,2).
如图,点A的坐标为(-2,3),向量$\overrightarrow{a}$的模为4,则向量$\overrightarrow{OA}$的坐标为(-2,3),向量$\overrightarrow{a}$的坐标为(2$\sqrt{3}$,2).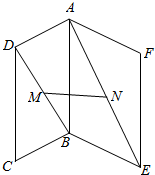 如图,边长相等的两个正方形ABCD和ABEF所在平面相交于AB,M∈BD,N∈AE且BM=EN≠BD.求证:MN⊥AB.
如图,边长相等的两个正方形ABCD和ABEF所在平面相交于AB,M∈BD,N∈AE且BM=EN≠BD.求证:MN⊥AB.