题目内容
设函数f(x)＝sinx＋cosx，f ′(x)是f(x)的导数，若f(x)＝2f ′(x)，则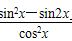
＝________.
－
[解析] ∵f(x)＝sinx＋cosx，∴f ′(x)＝cosx－sinx，
∴sinx＋cosx＝2(cosx－sinx)，
即3sinx＝cosx，得tanx＝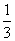
，
于是
＝tan2x－2tanx＝
－
＝－.
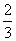练习册系列答案
相关题目
题目内容
设函数f(x)＝sinx＋cosx，f ′(x)是f(x)的导数，若f(x)＝2f ′(x)，则＝________.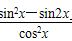
－
[解析] ∵f(x)＝sinx＋cosx，∴f ′(x)＝cosx－sinx，
∴sinx＋cosx＝2(cosx－sinx)，
即3sinx＝cosx，得tanx＝，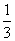
于是
＝tan2x－2tanx＝－＝－.
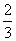在(
，＋∞)是增函数，则a的取值范围是( )
α是( )
＋α)＝
，那么cosα＝( )
B．－
，且α在第四象限，计算：
(n∈Z)．
，
)上是增加的
，
，则cos2(α＋
)＝( )
B.
C.
D.
，则AC＝( )
B．2