题目内容
(本小题满分14分)如图,在三棱锥 中,
中, ,点
,点 是线段
是线段 的中点,平面
的中点,平面 平面
平面 .
.

(1)在线段 上是否存在点
上是否存在点 , 使得
, 使得 平面
平面 ? 若存在, 指出点
? 若存在, 指出点 的位置, 并加以证明;若不存在, 请说明理由;
的位置, 并加以证明;若不存在, 请说明理由;
(2)求证: .
.
(1)在线段 上存在点
上存在点 ,使得
,使得 平面
平面 ,点
,点 是线段
是线段 的中点,证明详见解析;(2)证明详见解析.
的中点,证明详见解析;(2)证明详见解析.
【解析】
试题分析:本小题主要考查直线与平面的位置关系的基础知识,考查空间想象能力、推理论证能力和运算求解能力.对于(1)问,注意到点 ,
, 与直线
与直线 同在一个平面
同在一个平面 内,而面
内,而面 面
面 ,故在平面
,故在平面 内,过点
内,过点 作
作 ,直线
,直线 与线段
与线段 的交点就是
的交点就是 点,由条件不难知道
点,由条件不难知道 为
为 的中点,问题得以解决;(2)题中给出了较多边的长度,所以首先考虑这些边所组成的三角形
的中点,问题得以解决;(2)题中给出了较多边的长度,所以首先考虑这些边所组成的三角形 是否为直角三角形,根据勾股定理从而不难得出
是否为直角三角形,根据勾股定理从而不难得出 ,所以要证
,所以要证 ,就只须证明
,就只须证明 平面
平面 ,注意到题中还有一个条件平面
,注意到题中还有一个条件平面
 平面
平面 没有使用,结合平面
没有使用,结合平面
 平面
平面
 及
及 ,就不难得出
,就不难得出 平面
平面 ,命题得证.
,命题得证.
试题解析:(1)在线段 上存在点
上存在点 ,使得
,使得 平面
平面 ,点
,点 是线段
是线段 的中点 2分
的中点 2分
下面证明 平面
平面 :
:
取线段 的中点
的中点 ,连接
,连接 , 3分
, 3分

∵点 是线段
是线段 的中点
的中点
∴ 是△
是△ 的中位线 4分
的中位线 4分
∴ 6分
6分
∵ 平面
平面 ,
, 平面
平面
∴ 平面
平面 8分
8分
(2)证明:∵
∴
∴ 10分
10分
∵平面
 平面
平面 ,且平面
,且平面
 平面
平面
 ,
, 平面
平面
∴ 平面
平面 12分
12分
∵ 平面
平面
∴ 14分.
14分.
考点:1.空间中的平行关系;2.空间中的垂直关系——线线垂直、线面垂直,面面垂直的判定与性质.

练习册系列答案
相关题目
 中,已知椭圆
中,已知椭圆 :
: ,设
,设 是椭圆
是椭圆 上的任一点,从原点
上的任一点,从原点 向圆
向圆 :
: 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点 ,
, .
.
 ,
, 互相垂直,求圆
互相垂直,求圆 ,
, ,求证:
,求证: ;
; 是否为定值?若是,求出该值;若不是,说明理由.
是否为定值?若是,求出该值;若不是,说明理由. 的最小正周期为( )
的最小正周期为( ) B.
B. C.
C. D.
D.
 ,
, ,且
,且 在区间
在区间 上递减,则
上递减,则 ( )
( )
 中, 点
中, 点 关于原点
关于原点 的对称点的坐标为 .
的对称点的坐标为 .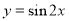 是( )
是( )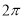 的偶函数
的偶函数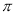 的偶函数
的偶函数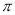 的奇函数
的奇函数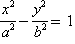 (a>0,b>0),若过右焦点F且倾斜角为30°的直线与双曲线的右支有
(a>0,b>0),若过右焦点F且倾斜角为30°的直线与双曲线的右支有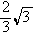 ) C.[2,+∞) D.[
) C.[2,+∞) D.[ ,
, ,则△ABC的面积等于 .
,则△ABC的面积等于 .