题目内容
求下列函数的单调区间:
(1)y=sin(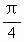 -2x);(2)y=
-2x);(2)y=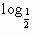 cos(
cos(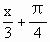 ).
).
答案:
解析:
解析:
|
解 (1)此题可看作是由y=sint和t= 略解 由 |

练习册系列答案
相关题目
 -2x复合成的复合函数,应注意t=
-2x复合成的复合函数,应注意t= ≤
≤ ,∴-kπ-
,∴-kπ- ≤x≤-kπ+
≤x≤-kπ+ (k∈Z),∴函数y的单调递减区间是[kπ-
(k∈Z),∴函数y的单调递减区间是[kπ- (k∈Z).∴函数y的单调递增区间是[kπ-
(k∈Z).∴函数y的单调递增区间是[kπ- ,kπ-
,kπ- ](k∈Z).此题也可将函数改写成y=-sin(2x-
](k∈Z).此题也可将函数改写成y=-sin(2x- )的形式,然后求解.(2)此题应注意两个方面,首先是对数应有意义,cos(
)的形式,然后求解.(2)此题应注意两个方面,首先是对数应有意义,cos( )>0,其次是以
)>0,其次是以 为底的对数函数是减函数.
为底的对数函数是减函数. (k∈Z).由2kπ≤
(k∈Z).由2kπ≤ (k∈Z),∴单调递增区间是[6kπ-
(k∈Z),∴单调递增区间是[6kπ- ,6kπ+
,6kπ+ )(k∈Z);单调递减区间是(6kπ-
)(k∈Z);单调递减区间是(6kπ- ,6kπ-
,6kπ- ; (2)y=
; (2)y= tan2x+1;
tan2x+1;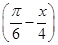 .
.