题目内容
如图,在三棱锥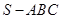 中,平面
中,平面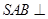 平面
平面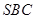 ,
,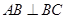 ,
,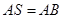 . 过点
. 过点 作
作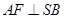 ,垂足为
,垂足为 ,点
,点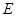 ,
,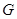 分别为棱
分别为棱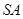 ,
,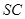 的中点.
的中点.

求证:(1)平面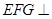 平面
平面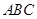 ;
;
(2)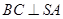 .
.
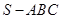 中,平面
中,平面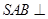 平面
平面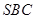 ,
,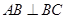 ,
,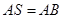 . 过点
. 过点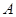 作
作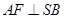 ,垂足为
,垂足为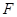 ,点
,点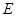 ,
,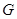 分别为棱
分别为棱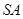 ,
,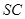 的中点.
的中点.
求证:(1)平面
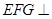 平面
平面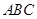 ;
;(2)
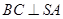 .
.见解析
[证明] (1)∵
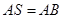 ,
,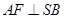 ,垂足为
,垂足为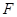 ,∴
,∴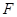 是
是 的中点,又因为
的中点,又因为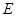 是
是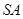 的中点,
的中点,∴
 ∥
∥ ,∵
,∵ 平面
平面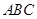 ,
, 平面
平面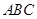 ,∴
,∴ ∥平面
∥平面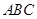 ;
;同理
 ∥平面
∥平面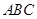 . 又
. 又 ,∴平面
,∴平面 ∥平面
∥平面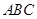 .
.(2)∵平面
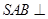 平面
平面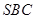 ,且交线为
,且交线为 ,又
,又 平面
平面 ,
,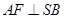 ,
,∴
 平面
平面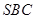 ,∵
,∵ 平面
平面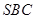 ,∴
,∴ ,
,又因为
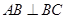 ,
, ,
, 、
、 平面
平面 ,
,∴
 平面
平面 ,∵
,∵ 平面
平面 ,∴
,∴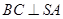 .
.【考点定位】本小题主要考查直线与直线、直线与平面以及平面与平面的位置关系,考查空间想象能力和推理论证能力.

练习册系列答案
相关题目
 的底面为矩形,
的底面为矩形, ,
, ,
, 分别是
分别是 的中点,
的中点, .
.
 平面
平面 ;
; 平面
平面 .
. 中,侧棱
中,侧棱 底面
底面 ,
,

 平面
平面
 与平面
与平面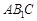 所成角的正弦值为
所成角的正弦值为 ,求
,求 的值
的值 ,写出
,写出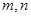 是两条不同的直线,
是两条不同的直线,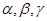 是三个不同的平面,下列命题中错误的是( )
是三个不同的平面,下列命题中错误的是( )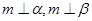 ,则
,则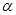 ∥
∥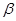
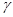 ,
,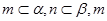 ∥
∥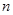 ,则
,则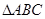 是边长为2的正三角形,
是边长为2的正三角形,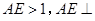 平面ABC,平面
平面ABC,平面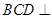 平面ABC,BD=CD,且
平面ABC,BD=CD,且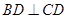 .
.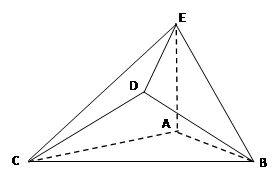
 的正方体
的正方体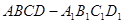 中,错误的是( )
中,错误的是( )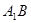 和直线
和直线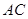 所成角的大小为
所成角的大小为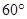
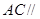 平面
平面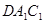
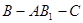 的大小是
的大小是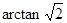
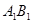 到平面
到平面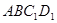 的距离为
的距离为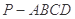 中,底面
中,底面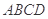 为正方形,
为正方形,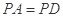
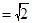 ,
,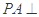 平面
平面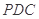 ,
,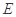 为棱
为棱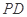 的中点.
的中点.
 平面
平面 ;
; 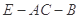 的余弦值.
的余弦值. 到平面
到平面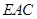 的距离.
的距离.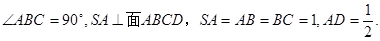
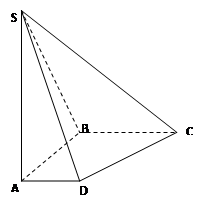
 ,其边长为2,
,其边长为2, ,
,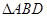 绕着
绕着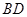 顺时针旋转
顺时针旋转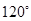 得到
得到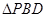 ,
,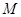 是
是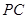 的中点.
的中点.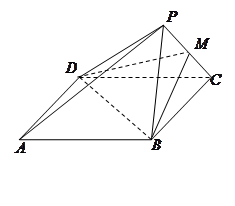
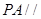 平面
平面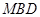 ;
;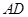 与平面
与平面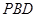 所成角的正弦值.
所成角的正弦值.