题目内容
已知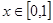 ,函数
,函数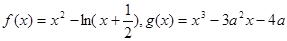 .
.
(1)求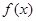 的单调区间和值域;
的单调区间和值域;
(2)设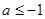 ,若
,若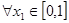 ,总
,总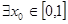 ,使得
,使得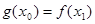 成立,求
成立,求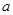 的取值范围;
的取值范围;
(3)对于任意的正整数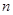 ,证明:
,证明: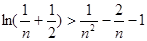 .
.
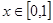 ,函数
,函数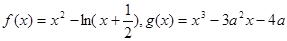 .
.(1)求
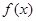 的单调区间和值域;
的单调区间和值域;(2)设
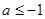 ,若
,若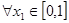 ,总
,总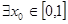 ,使得
,使得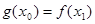 成立,求
成立,求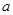 的取值范围;
的取值范围;(3)对于任意的正整数
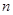 ,证明:
,证明: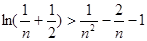 .
.(1)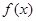 单调减区间
单调减区间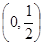 ,
,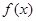 单调增区间
单调增区间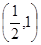 ,
,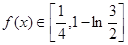 (2)
(2)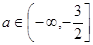 ;(3)略
;(3)略
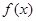 单调减区间
单调减区间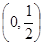 ,
,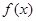 单调增区间
单调增区间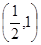 ,
,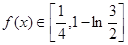 (2)
(2)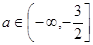 ;(3)略
;(3)略本试题主要考查了导数在研究函数中的运用。
解 (1)令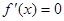 ,解得
,解得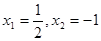 (舍去),
(舍去),
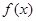 单调减区间
单调减区间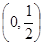 ,
,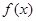 单调增区间
单调增区间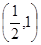 ,
,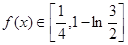 ;…… 4分
;…… 4分
(2)∵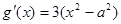 ,
,
∴当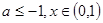 时
时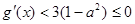 ,…………………6分
,…………………6分
∴ 为
为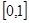 上的减函数,从而当
上的减函数,从而当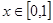 时有
时有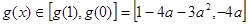 ,…8分
,…8分
由题意知: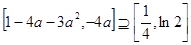 ,
,
即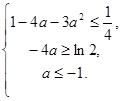 故
故 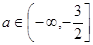 ;………………… 10分
;………………… 10分
(3)构造函数: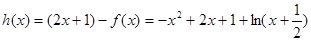 ,
,
则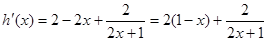 ,………………… 11分
,………………… 11分
当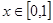 时,
时,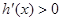 ,∴函数
,∴函数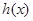 在
在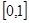 上单调增,………………… 12分
上单调增,………………… 12分
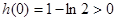 ∴
∴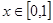 时,恒有
时,恒有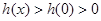 ,……13分
,……13分
即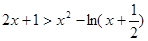 恒成立,…………………14分
恒成立,…………………14分
故对任意正整数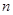 ,取
,取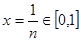 有
有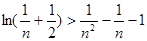 .
.
解 (1)令
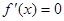 ,解得
,解得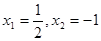 (舍去),
(舍去), 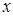 | 0 | (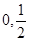 ) ) | 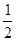 | (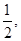 1) 1) | 1 |
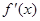 | | __ | 0 | + | |
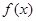 | 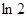 | ↘ | 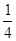 | ↗ | 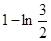 |
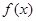 单调减区间
单调减区间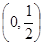 ,
,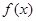 单调增区间
单调增区间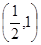 ,
,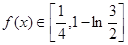 ;…… 4分
;…… 4分(2)∵
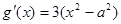 ,
,∴当
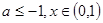 时
时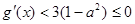 ,…………………6分
,…………………6分∴
 为
为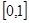 上的减函数,从而当
上的减函数,从而当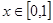 时有
时有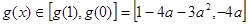 ,…8分
,…8分由题意知:
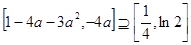 ,
,即
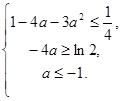 故
故 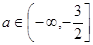 ;………………… 10分
;………………… 10分(3)构造函数:
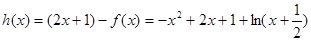 ,
,则
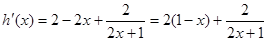 ,………………… 11分
,………………… 11分当
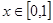 时,
时,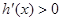 ,∴函数
,∴函数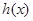 在
在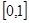 上单调增,………………… 12分
上单调增,………………… 12分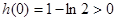 ∴
∴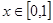 时,恒有
时,恒有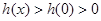 ,……13分
,……13分即
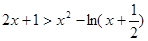 恒成立,…………………14分
恒成立,…………………14分故对任意正整数
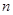 ,取
,取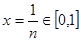 有
有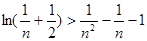 .
.
练习册系列答案
相关题目
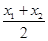 时,又称AB存在“中值伴随切线”.试问:在函数f(x)的图像上是否存在不同两点A,B,使得AB存在“中值伴随切线”?若存在,求出A,B的坐标;若不存在,说明理由
时,又称AB存在“中值伴随切线”.试问:在函数f(x)的图像上是否存在不同两点A,B,使得AB存在“中值伴随切线”?若存在,求出A,B的坐标;若不存在,说明理由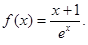
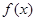 的单调区间;
的单调区间;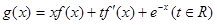 ,是否存在实数a、b、c∈[0,1],使得
,是否存在实数a、b、c∈[0,1],使得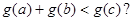 若存在,求出t的取值范围;若不存在,说明理由.
若存在,求出t的取值范围;若不存在,说明理由.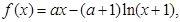 其中
其中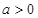 ,
,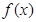 的单调区间;
的单调区间;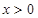 时,证明不等式:
时,证明不等式: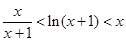 .
.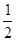 +
+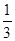 +
+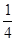 +L
+L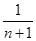 (
( ).
).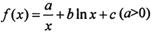 的图象在点(1, f(1))处的切线方程为x-y-2=0
的图象在点(1, f(1))处的切线方程为x-y-2=0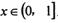 上的最大值为2,求实数a的取值范围.
上的最大值为2,求实数a的取值范围. ,
, .
.  时,求函数
时,求函数 的极值;
的极值; 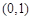 上是单调增函数,求实数
上是单调增函数,求实数 的取值范围.
的取值范围.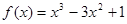 是减函数的区间为( )
是减函数的区间为( )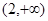
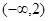
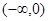
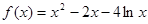 ,则
,则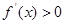 的解集为( )
的解集为( )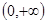
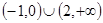
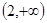
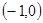
 的单调递增区间是
的单调递增区间是