题目内容
2.一艘轮船在江中向正东方向航行,在点P处观测到灯塔A、B在一直线上,并且此直线与航行方向成30°角,轮船沿航线前进600米到达C处,此时观测到灯塔A在北偏西45°方向,灯塔B在北偏东15°方向.求两灯塔之间的距离.分析 先根据条件求出题中所涉及到的角,再根据正弦定理分别求出PB,PA,即可得到结论.
解答 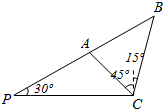 解:由题得:PC=600,∠ACP=45°,∠PAC=105°,∠PCB=105°,∠PBC=45°.
解:由题得:PC=600,∠ACP=45°,∠PAC=105°,∠PCB=105°,∠PBC=45°.
在△BCP中,$\frac{PB}{sin∠PCB}$=$\frac{PC}{sin∠PBC}$⇒PB=PC•$\frac{sin105°}{sin45°}$=300+300$\sqrt{3}$;
在△ACP中,$\frac{PC}{sin∠PAC}=\frac{PA}{sin∠PCA}$⇒PA=PC•$\frac{sin45°}{sin105°}$=600×($\sqrt{3}$-1);
∴AB=PB-PA=300+300$\sqrt{3}$-600($\sqrt{3}$-1)=900-300$\sqrt{3}$.
点评 本题主要考查解三角形的实际应用.一般解决这类问题时用正弦定理或余弦定理,本题主要涉及到正弦定理的运用以及特殊角的三角函数值.

练习册系列答案
相关题目
12.集合P={x|y=$\sqrt{x+1}$},Q={y|y=$\sqrt{x+1}$},则P,Q的关系是( )
| A. | P=Q | B. | P?Q | C. | Q?P | D. | P∩Q=∅ |
10.命题p:若随机事件A,B是对立事件,则A,B一定是互斥事件,则¬P是( )
| A. | 若随机事件A,B是对立事件,则A,B一定不是互斥事件 | |
| B. | 若随机事件A,B不是对立事件,则A,B一定不是互斥事件 | |
| C. | 存在随机事件A,B是对立事件,并且A,B不是互斥事件 | |
| D. | 存在随机事件A,B不是对立事件,并且A,B是互斥事件 |