题目内容
20.?t∈R,不等式|2x-2|+4x<|t-3|+|t-4|恒成立.(1)求实数x的取值范围M.
(2)设a,b∈M,比较|1-4ab|与2|a-b|的大小,并说明理由.
分析 (1)利用绝对值三角不等式求得,|t-3|+|t-4|的最小值为1,可得|2x-2|+4x<1,去掉绝对值,分类讨论,求得x的范围.
(2)根据a,b∈M,可得a<-$\frac{1}{2}$,b<-$\frac{1}{2}$,故有4ab>1,可得|1-4ab|=4ab-1,分a≥b和a<b两种情况,分别较|1-4ab|与2|a-b|的大小关系,综合可得结论.
解答 解:(1)∵?t∈R,不等式|2x-2|+4x<|t-3|+|t-4|恒成立,|t-3|+|t-4|≥|t-3-(t-4)|=1,
∴应有|2x-2|+4x<1,∴$\left\{\begin{array}{l}{x≥1}\\{2x-2+4x<1}\end{array}\right.$ ①,或$\left\{\begin{array}{l}{x<1}\\{2-2x+4x<1}\end{array}\right.$②.
解①求得x∈∅,解②求得x<-$\frac{1}{2}$.
综上可得,实数x的取值范围M={x|x<-$\frac{1}{2}$}.
(2)∵a,b∈M,则a<-$\frac{1}{2}$,b<-$\frac{1}{2}$,∴ab>$\frac{1}{4}$,4ab>1,∴|1-4ab|=4ab-1.
当a≥b时,|1-4ab|-2|a-b|=4ab-1-2(a-b)=4ab+2b-2a-1=2b(2a+1)-(2a+1)=(2a+1)(2b-1),
∵2a<-1,2b<-1,∴2a+1<0,2b-1<0,∴(2a+1)(2b-1)>0,∴|1-4ab|>-2|a-b|.
当a<b时,|1-4ab|-2|a-b|=4ab-1+2(a-b)=4ab-2b+2a-1=2b(2a-1)+(2a-1)=(2a-1)(2b+1),
∵2a<-1,2b<-1,∴2a-1<0,2b+1<0,∴(2a+1)(2b-1)>0,∴|1-4ab|>-2|a-b|.
综上可得,|1-4ab|>-2|a-b|.
点评 本题主要考查绝对值三角不等式的应用,函数的恒成立问题,体现了分类讨论的数学思想,属于中档题.

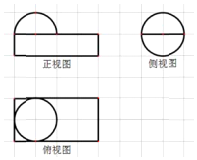
| A. | $\frac{14π}{3}$ | B. | $\frac{10π}{3}$ | C. | $\frac{8π}{3}$ | D. | $\frac{5π}{3}$ |
| A. | b>a>c | B. | b>c>a | C. | c>a>b | D. | a>b>c |
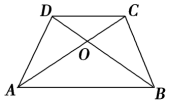 如图所示,梯形ABCD的对角线交于点O,则下列四个结论:
如图所示,梯形ABCD的对角线交于点O,则下列四个结论:①△AOB∽△COD;
②△AOD∽△ACB;
③S△DOC:S△AOD=CD:AB;
④S△AOD=S△BOC.
其中正确的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | {x|0<x<2} | B. | ∅ | C. | {0,2} | D. | {x|x≤0或x=2} |