题目内容
8．若x，y满足$\left\{\begin{array}{l}{1＜x＜6}\\{2＜y＜8}\end{array}\right.$，则$\frac{x}{y}$的取值范围是$（\frac{1}{8}，3）$．分析 由2＜y＜8，可得$\frac{1}{8}＜\frac{1}{y}＜\frac{1}{2}$，又1＜x＜6．利用不等式的基本性质即可得出．
解答 解：由2＜y＜8，可得$\frac{1}{8}＜\frac{1}{y}＜\frac{1}{2}$，又1＜x＜6．
∴$\frac{1}{8}＜\frac{x}{y}＜3$．
∴$\frac{x}{y}$的取值范围是$（\frac{1}{8}，3）$．
故答案为：$（\frac{1}{8}，3）$．
点评 本题考查了不等式的基本性质，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
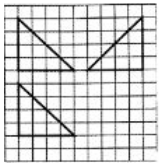如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，若该几何体的各个顶点在某一个球面上，则该球面的表面积为48π．