题目内容
已知函数f（x）=a•2x+b的图象经过点（1，2），其反函数的图象经过点（6，2），则a+b= ．
考点：指数函数的单调性与特殊点,反函数
专题：函数的性质及应用
分析：根据指数函数的性质以及反函数的关系建立方程关系即可得到结论．
解答：
解：∵函数f（x）的反函数的图象经过点（6，2），
∴函数f（x）的图象过点（2，6），
即f（2）=6，则4a+b=6，①
∵函数f（x）=a•2x+b的图象经过点（1，2），
∴f（1）=2，则2a+b=2，②
由①②得a=2，b=-2，
则a+b=2-2=0，
故答案为：0；
∴函数f（x）的图象过点（2，6），
即f（2）=6，则4a+b=6，①
∵函数f（x）=a•2x+b的图象经过点（1，2），
∴f（1）=2，则2a+b=2，②
由①②得a=2，b=-2，
则a+b=2-2=0，
故答案为：0；
点评：本题主要考查指数函数的图象和性质，利用反函数的性质求出函数f（x）过点（2，6）是解决本题的关键．
练习册系列答案
相关题目
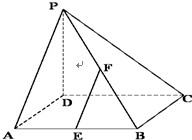如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD为正方形，PD=DC，E，F分别是AB，PB的中点．