题目内容
若点P在△AOB的边AB上,且 =m
=m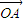 +4n
+4n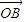 (m,n∈R),则mn的最大值为 .
(m,n∈R),则mn的最大值为 .
【答案】分析:求出 和
和  ,由
,由  ∥
∥ ,可得 m+4n=1,利用基本不等式可得 mn≤
,可得 m+4n=1,利用基本不等式可得 mn≤ ,从而得到答案.
,从而得到答案.
解答:解:∵ =
= -
- =(m-1)
=(m-1) +4n
+4n ,
, =
= -
- =-m
=-m +(1-4n)
+(1-4n) ,
,
由于点P在△AOB的边AB上,故m、n 都是正数,且 ∥
∥ ,∴(m-1)(1-4n)-4n(-m)=0,
,∴(m-1)(1-4n)-4n(-m)=0,
化简可得 m+4n=1,由基本不等式可得 1≥2 ,∴mn≤
,∴mn≤ ,当且仅当 m=4n=
,当且仅当 m=4n= 时,
时,
等号成立,故mn的最大值为 ,
,
故答案为: .
.
点评:本题考查两个向量共线的性质,两个向量坐标形式的运算,基本不等式的应用,注意基本不等式的使用条件,并注意检验等号成立的条件.
 和
和  ,由
,由  ∥
∥ ,可得 m+4n=1,利用基本不等式可得 mn≤
,可得 m+4n=1,利用基本不等式可得 mn≤ ,从而得到答案.
,从而得到答案.解答:解:∵
 =
= -
- =(m-1)
=(m-1) +4n
+4n ,
, =
= -
- =-m
=-m +(1-4n)
+(1-4n) ,
,由于点P在△AOB的边AB上,故m、n 都是正数,且
 ∥
∥ ,∴(m-1)(1-4n)-4n(-m)=0,
,∴(m-1)(1-4n)-4n(-m)=0,化简可得 m+4n=1,由基本不等式可得 1≥2
 ,∴mn≤
,∴mn≤ ,当且仅当 m=4n=
,当且仅当 m=4n= 时,
时,等号成立,故mn的最大值为
 ,
,故答案为:
 .
.点评:本题考查两个向量共线的性质,两个向量坐标形式的运算,基本不等式的应用,注意基本不等式的使用条件,并注意检验等号成立的条件.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
△OAB中,
=
,
=
,
=
,若
=t(
+
),t∈R,则点P一定在( )
| OA |
| a |
| OB |
| b |
| OP |
| p |
| p |
| ||
|
|
| ||
|
|
| A、∠AOB平分线所在直线上 |
| B、线段AB中垂线上 |
| C、AB边所在直线上 |
| D、AB边的中线上 |
 =m
=m +4n
+4n (m,n∈R),则mn的最大值为________.
(m,n∈R),则mn的最大值为________.